题目内容
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且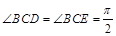 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.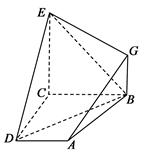
(1)求证:AG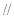 平面BDE;
平面BDE;
(2)求:二面角G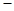 DE
DE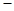 B的余弦值.
B的余弦值.
(1)见解析(2)
解析试题分析:(1)由题设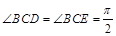 ,平面ABCD⊥平面BCEG,可证
,平面ABCD⊥平面BCEG,可证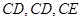 两两垂直,据此建设立以
两两垂直,据此建设立以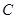 为坐标原点的空间直角坐标系,写出
为坐标原点的空间直角坐标系,写出 诸点的坐标,求出平面
诸点的坐标,求出平面 的一个法向量
的一个法向量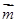 ,由于
,由于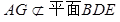 ,要证AG
,要证AG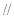 平面BDE,只要证
平面BDE,只要证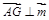 即可;
即可;
(2)设平面 的一个法向量为
的一个法向量为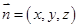 ,由
,由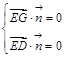 求出的坐标,最后利用向量
求出的坐标,最后利用向量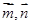 求出二面角G
求出二面角G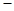 DE
DE B的余弦值.
B的余弦值.
试题解析:
解:由平面 ,平面
,平面 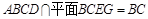 ,
, 平面BCEG,
平面BCEG, 
 ,
,
由平面 ,
,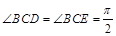 知
知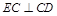 ,.2分
,.2分
根据题意建立如图所示的空间直角坐标系,可得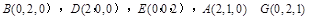 .3分
.3分
(1)设平面BDE的法向量为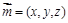 ,则
,则
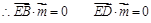
 即
即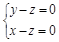 ,
, 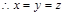 ,
, 平面BDE的一个法向量为
平面BDE的一个法向量为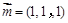 ..5分
..5分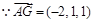
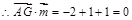 ,
, ,
,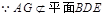 ,∴AG∥平面BDE. .7分
,∴AG∥平面BDE. .7分
(2)由(1)知
设平面EDG的法向量为 ,则
,则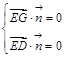 即
即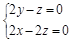
 平面EDG的一个法向量为
平面EDG的一个法向量为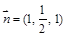 ..9分
..9分
又平面BDE的一个法向量为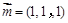 ,
,
设二面角 的大小为
的大小为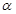 ,则
,则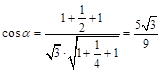 ,
, 二面角
二面角 的余弦值为
的余弦值为 .12分
.12分
考点:1、空间直角坐系;2、利用空间向量的数量积判断空间中直线与平面的位置关系;3、利用空间向量的夹角求二面角的平面角的余弦.

练习册系列答案
相关题目
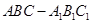 中,平面
中,平面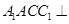 平面ABC,
平面ABC,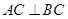 ,
,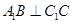 ,
,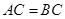 .
.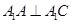 ;
;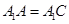 ,求二面角
,求二面角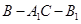 的余弦值.
的余弦值.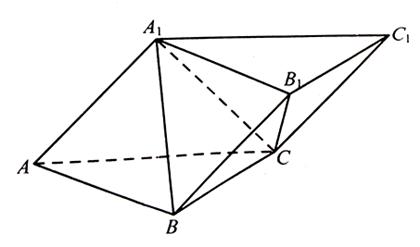
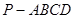 中,底面
中,底面 为平行四边形,
为平行四边形,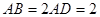 ,
,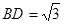 ,
,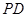 ⊥底面
⊥底面
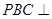 平面
平面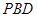 ;
; 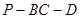 为
为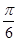 ,求
,求 与平面
与平面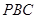 所成角的正弦值.
所成角的正弦值.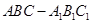 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是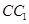 棱的中点,AE交
棱的中点,AE交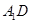 于点H.
于点H.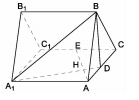
 平面
平面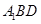 ;
;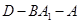 的余弦值;
的余弦值; 到平面
到平面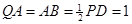 .
.

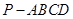 的底面
的底面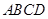 是等腰梯形,
是等腰梯形,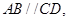 且
且
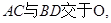
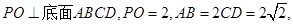
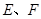 分别是
分别是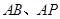 的中点.
的中点.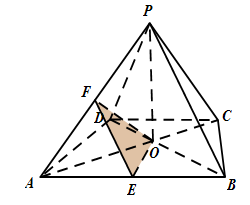
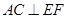 ;
;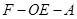 的余弦值.
的余弦值.
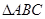 中,
中,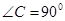 ,
, ,点
,点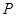 在边
在边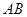 上,设
上,设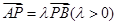 ,过点
,过点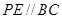 交
交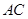 于
于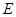 ,作
,作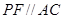 交
交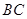 于
于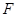 。沿
。沿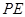 将
将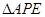 翻折成
翻折成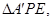 使平面
使平面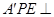 平面
平面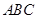 ;沿
;沿 将
将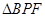 翻折成
翻折成 使平面
使平面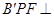 平面
平面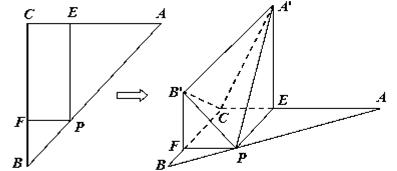
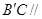 平面
平面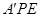 ;
;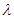 ,使得二面角
,使得二面角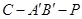 的大小为
的大小为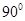 ?若存在,求出
?若存在,求出