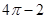题目内容
已知钝角△ABC的最长边为1,其余两边的长为a、b,则集合P={(x,y)|x=a,y=b}所表示的平面图形面积等于
.
| π-2 |
| 4 |
| π-2 |
| 4 |
分析:根据三角形两边之和大于第三边及由余弦定理得出a,b的不等关系,在坐标平面内画出不等关系所表示的图形即集合P={(x,y)|x=a,y=b}所表示的平面图形,最后求出其面积即可.
解答: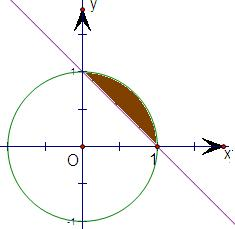 解:根据三角形两边之和大于第三边得:a+b>1,①
解:根据三角形两边之和大于第三边得:a+b>1,①
又由余弦定理得:cosC=
<0⇒a2+b2<1.②
在坐标平面内画出①②所表示的图形即集合P={(x,y)|x=a,y=b}所表示的平面图形,
如图阴影部分所示,
其面积是:
-
=
.
故答案为:
.
 解:根据三角形两边之和大于第三边得:a+b>1,①
解:根据三角形两边之和大于第三边得:a+b>1,①又由余弦定理得:cosC=
| a 2+b 2-1 |
| 2ab |
在坐标平面内画出①②所表示的图形即集合P={(x,y)|x=a,y=b}所表示的平面图形,
如图阴影部分所示,
其面积是:
| π |
| 4 |
| 1 |
| 2 |
| π-2 |
| 4 |
故答案为:
| π-2 |
| 4 |
点评:本小题主要考查二元一次不等式(组)与平面区域、余弦定理、三角形两边之和大于第三边等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
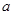 、
、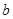 ,则集合
,则集合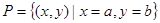 所表示的平面图形面积等于( )
所表示的平面图形面积等于( )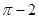 C.4 D.
C.4 D.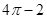
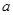 、
、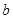 ,则集合
,则集合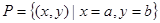 所表示的平面图形面积等于( )
所表示的平面图形面积等于( )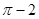 D.
D.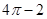
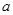 、
、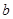 ,则集合
,则集合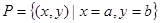 所表示的平面图形面积等于( )
所表示的平面图形面积等于( )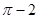 C.4 D.
C.4 D.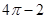
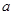 、
、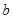 ,则集合
,则集合 所表示的平面图形面积等于( )
所表示的平面图形面积等于( )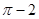 C.4 D.
C.4 D.