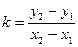题目内容
若曲线C:y=x3-2ax2+2ax上任意点处的切线的倾斜角都是锐角,那么整数a的值等于 ( )
| A.-2 | B.0 |
| C.1 | D.-1 |
C
根据倾斜角与斜率的关系,由曲线C:y=x3-2ax2+2ax上任意点处的切线的倾斜角都是锐角,得到斜率大于0,即函数的导函数大于0恒成立,即根的判别式小于0,列出关于x的不等式,求出不等式的解集即可得到a的取值范围,又因为a为整数,即可求出解集中的整数解得到a的值.
解:k=y′=3x2-4ax+2a,
由题设3x2-4ax+2a>0恒成立,
∴△=16a2-24a<0,
∴0<a<3/2,又a为整数,
∴a=1.
故选C.

练习册系列答案
相关题目
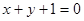 的倾斜角是( )
的倾斜角是( )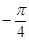
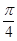
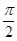
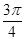
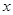 -6,则直线的倾斜角为
-6,则直线的倾斜角为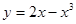 在点(1,1)处的切线方程为 .
在点(1,1)处的切线方程为 . 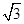 y-3=0的倾斜角是___ ___________
y-3=0的倾斜角是___ ___________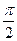
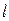 的倾斜角取值范围是第一象限角或第二象限角
的倾斜角取值范围是第一象限角或第二象限角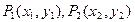 两点,则直线
两点,则直线