题目内容
已知向量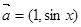 ,
,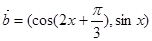 ,函数
,函数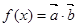
(1)求函数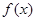 的解析式及其单调递增区间;
的解析式及其单调递增区间;
(2)在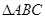 中,角
中,角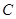 为钝角,若
为钝角,若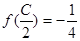 ,
,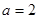 ,
,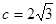 .求
.求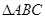 的面积。
的面积。
【答案】
(1)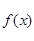
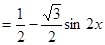 ,单调递增区间为
,单调递增区间为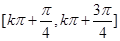 ,
,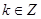 ;
;
(2)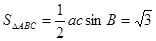 .
.
【解析】
试题分析:(1)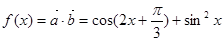
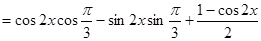
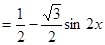
由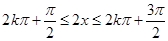 得:
得: 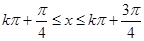
单调递增区间为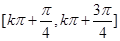 ,
,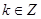 6分
6分
(2)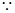
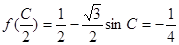 ,
,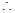
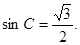
角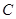 为钝角,所以
为钝角,所以 8分
8分
由正弦定理可得: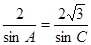 ,
,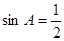 ,而
,而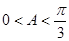
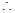
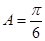 ,
,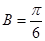 10分
10分
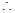
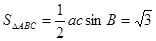 12分
12分
考点:本题主要考查平面向量的数量积,平面向量的坐标运算,正弦定理、余弦定理的应用,和差倍半的三角函数公式。
点评:典型题,属于常见题型,根据已知条件,灵活运用数量积及三角公式化简,并进一步研究正弦型函数的性质。综合应用正弦定理、余弦定理,得到三角形边角关系,利用三角形面积公式,达到解题目的。

练习册系列答案
相关题目
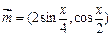 ,
, ,函数
,函数
 的最小正周期;
的最小正周期;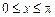 ,求
,求










 ,
, ,函数
,函数 .
. ,
, ,函数
,函数 .
. 在
在 上有解,求
上有解,求 的取值范围;
的取值范围; 中,
中, 分别是A,B,C所对的边,当(Ⅰ)中的
分别是A,B,C所对的边,当(Ⅰ)中的 时,求
时,求 的最小值.
的最小值. ,
, ,函数
,函数 .
. 的最小正周期以及单调递增区间;
的最小正周期以及单调递增区间; 时, 求
时, 求 在
在 内的所有实数根之和.
内的所有实数根之和.