题目内容
等差数列{an}中,a1=1,a7=4,在等比数列{bn}中,b1=6,b2=a3,则满足bna26<1的最小正整数n是 .
6
解析试题分析:因为等差数列{an}中,a1=1,a7=4,那么可知1+6d=4,d=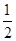 ,
,
∵数列{bn}是等比数列,且b1=6,b2=a3,∴6q=1+2×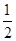 ,解得q=
,解得q=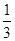 ,因为∵bna26<1,
,因为∵bna26<1,
即可知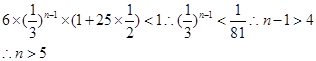
故最小的正整数为6,故答案为6.
考点:本题考查数列和不等式的综合。
点评:该试题考查等差数列、等比数列的基本量、通项,对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
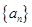 中,
中,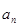 >0,若
>0,若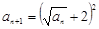 ,
,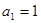 ,则该数列的通项
,则该数列的通项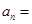 ____
____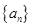 中,
中,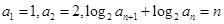 (
(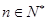 ),则
),则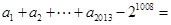 .
.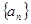 中,
中,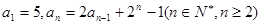 ,若存在实数
,若存在实数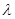 ,使得数列
,使得数列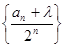 为等差数列,则
为等差数列,则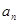 }的首项
}的首项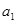 =2,
=2,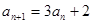 ,数列{
,数列{ .
.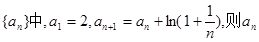 =
= 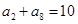 ,前
,前 项和为
项和为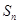 ,则
,则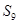 = .
= .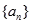 的首项
的首项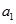 及公差
及公差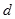 都是整数,前
都是整数,前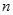 项和为
项和为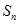 ,若
,若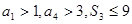 ,设
,设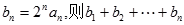 的结果为 。
的结果为 。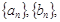
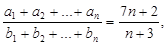 则
则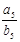 =___________.
=___________.