题目内容
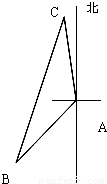
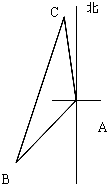 如图所示,我舰在敌岛A南偏西50° 且与A相距6海里的B处,发现敌舰正由岛A沿北偏西10°的方向以5海里/小时的速度航行,我舰要用2小时在C处追上敌舰,问需要的速度是多少?
如图所示,我舰在敌岛A南偏西50° 且与A相距6海里的B处,发现敌舰正由岛A沿北偏西10°的方向以5海里/小时的速度航行,我舰要用2小时在C处追上敌舰,问需要的速度是多少?分析:利用方向角,求得∠CAB=120°,利用余弦定理即可求得BC,然后求出需要的速度.
解答: 解:我舰2小时后在C处追上敌舰,即AC=2×5=10海里.
解:我舰2小时后在C处追上敌舰,即AC=2×5=10海里.
∵AB=6,∠CAB=180°-(50°+10°)=120°,
∴BC2=AC2+AB2-2AC•AB•cos120°=102+62-2×10×6•(-
)=196,
∴BC=14(海里),
∴需要的速度v=
=7(海里/小时).
答:需要的速度为每小时7海里.
 解:我舰2小时后在C处追上敌舰,即AC=2×5=10海里.
解:我舰2小时后在C处追上敌舰,即AC=2×5=10海里.∵AB=6,∠CAB=180°-(50°+10°)=120°,
∴BC2=AC2+AB2-2AC•AB•cos120°=102+62-2×10×6•(-
| 1 |
| 2 |
∴BC=14(海里),
∴需要的速度v=
| 14 |
| 2 |
答:需要的速度为每小时7海里.
点评:本题考查余弦定理,求得∠CAB是关键,考查分析与运算能力,属于中档题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
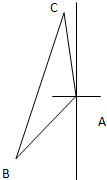 如图所示,我舰在敌岛A南偏西50° 相距12海里的B处,发现敌舰正由岛A沿北偏西10°的方向以时速10海里航行,我舰要用2小时在C处追上敌舰,问需要的速度是多少?
如图所示,我舰在敌岛A南偏西50° 相距12海里的B处,发现敌舰正由岛A沿北偏西10°的方向以时速10海里航行,我舰要用2小时在C处追上敌舰,问需要的速度是多少?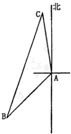 如图所示,我舰在敌岛A南偏西50°相距12海里的B处,发现敌舰正由岛A沿北偏西10°的方向以每小时10海里的速度航行,我舰要用2小时在C处追上敌舰,则需要的速度是
如图所示,我舰在敌岛A南偏西50°相距12海里的B处,发现敌舰正由岛A沿北偏西10°的方向以每小时10海里的速度航行,我舰要用2小时在C处追上敌舰,则需要的速度是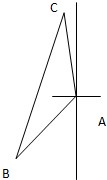 如图所示,我舰在敌岛A南偏西50° 相距12海里的B处,发现敌舰正由岛A沿北偏西10°的方向以时速10海里航行,我舰要用2小时在C处追上敌舰,问需要的速度是多少?
如图所示,我舰在敌岛A南偏西50° 相距12海里的B处,发现敌舰正由岛A沿北偏西10°的方向以时速10海里航行,我舰要用2小时在C处追上敌舰,问需要的速度是多少?