题目内容
已知函数 的图象是一个中心对称图形,则f(x)图象的对称中心坐标为 .
的图象是一个中心对称图形,则f(x)图象的对称中心坐标为 .
【答案】分析:由题意设出图象的对称中心的坐标,列出满足的恒等式,代入函数解析式列出方程,根据方程两边对应系数相等求出a和b的值
解答:解:由题意设对称中心的坐标为(a,b),
当x=1时,y=log23,当x=2时,y=0,
这两个点关于(a,b)对称的点也满足函数的解析式,
即(2a-1,2b-log23)(2a-2,-b)满足函数的解析式,
∴2b-log23=
-b=
∴a= ,b=-1,
,b=-1,
∴图形的对称中心的坐标是( ,-1)
,-1)
故答案为:( ,-1)
,-1)
点评:本题考查了函数图象中心对称的性质的应用,即函数的对称中心的坐标是(a,b),可以用2b=f(a+x)+f(a-x)对任意x均成立,由此恒等式进行求值.
解答:解:由题意设对称中心的坐标为(a,b),
当x=1时,y=log23,当x=2时,y=0,
这两个点关于(a,b)对称的点也满足函数的解析式,
即(2a-1,2b-log23)(2a-2,-b)满足函数的解析式,
∴2b-log23=
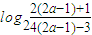
-b=
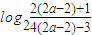
∴a=
 ,b=-1,
,b=-1,∴图形的对称中心的坐标是(
 ,-1)
,-1)故答案为:(
 ,-1)
,-1)点评:本题考查了函数图象中心对称的性质的应用,即函数的对称中心的坐标是(a,b),可以用2b=f(a+x)+f(a-x)对任意x均成立,由此恒等式进行求值.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 的图象是一条连续的曲线,满足
的图象是一条连续的曲线,满足 ,下列说法正确的是( )
,下列说法正确的是( ) 在
在 上至少有一个零点; B.
上至少有一个零点; B.