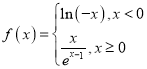题目内容
【题目】已知函数![]() .
.
(1)求![]() 时,
时,![]() 的单调区间;
的单调区间;
(2)若存在![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() ,求
,求![]() 的取值范围,并证明
的取值范围,并证明![]() .
.
【答案】(1)![]() 在
在![]() 为减函数,
为减函数,![]() 为增函数;(2)
为增函数;(2)![]() ,证明见解析
,证明见解析
【解析】
(1)由![]() 得
得![]() ,对函数求导,得到
,对函数求导,得到![]() , 令
, 令![]() ,用导数法方法判断其单调性,求出
,用导数法方法判断其单调性,求出![]() 在
在![]() 上为增函数,再由
上为增函数,再由![]() ,即可求出结果;
,即可求出结果;
(2)先对函数求导,得到 ,根据题意,得到
,根据题意,得到![]() 为
为![]() 在
在![]() 的极小值点,故
的极小值点,故![]() ,设
,设![]() ,对函数求导,根据函数单调性,得到
,对函数求导,根据函数单调性,得到 ,推出
,推出![]() ,再令
,再令![]() ,用导数的方法求出其单调性,进而可得出结果.
,用导数的方法求出其单调性,进而可得出结果.
(1)当![]() 时,
时,![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() ,由
,由![]() 得
得![]() ;由
;由![]() 得
得![]() ,
,
即函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因此![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
即![]() 在
在![]() 上为增函数.
上为增函数.
又因为![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
故![]() 在
在![]() 为减函数,
为减函数,![]() 为增函数.
为增函数.
(2)  ,
,
因为![]() 对任意的
对任意的![]() 恒成立,所以
恒成立,所以![]() 为
为![]() 在
在![]() 的极小值点,故
的极小值点,故![]() ①.
①.
设![]() ,则当
,则当![]() 时,
时, ,
,
所以![]() 在
在![]() 上为增函数,而
上为增函数,而![]() ,
,![]() .
.
由①可知![]() ,从而
,从而![]() ,故
,故![]() .
.
又由 ,即
,即 ,
,
所以
![]() .
.
令![]() ,其中
,其中![]() ,则
,则![]() ,
,![]() 为
为![]() 上的减函数,
上的减函数,
故![]() ,而
,而![]() ,
,
所以![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取![]() 个,利用水果的等级分类标准得到的数据如下:
个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)若将频率视为概率,从这![]() 个水果中有放回地随机抽取
个水果中有放回地随机抽取![]() 个,求恰好有
个,求恰好有![]() 个水果是礼品果的概率;(结果用分数表示)
个水果是礼品果的概率;(结果用分数表示)
(2)用分层抽样的方法从这![]() 个水果中抽取
个水果中抽取![]() 个,再从抽取的
个,再从抽取的![]() 个水果中随机抽取
个水果中随机抽取![]() 个,
个,![]() 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.