题目内容
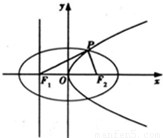
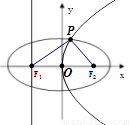
如图所示,设抛物线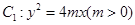 的焦点为
的焦点为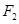 ,且其准线与
,且其准线与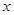 轴交于
轴交于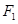 ,以
,以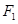 ,
,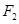 为焦点,离心率
为焦点,离心率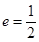 的椭圆
的椭圆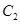 与抛物线
与抛物线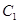 在
在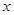 轴上方的一个交点为P.
轴上方的一个交点为P.
(1)当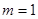 时,求椭圆
时,求椭圆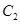 的方程;
的方程;
(2)是否存在实数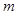 ,使得
,使得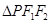 的三条边的边长是连续的自然数?若存在,求出这样的实数
的三条边的边长是连续的自然数?若存在,求出这样的实数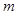 ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】
(1)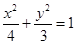 ;(2)
;(2)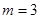 .
.
【解析】
试题分析:(1)依题意由抛物线方程容易得椭圆的方程,代入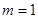 既得椭圆方程;(2)假设存在满足条件的实数
既得椭圆方程;(2)假设存在满足条件的实数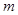
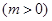 ,由抛物线和椭圆方程求交点P,使得
,由抛物线和椭圆方程求交点P,使得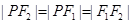 ,求得
,求得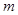 .
.
试题解析:(1)抛物线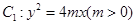 的焦点为
的焦点为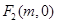 ,
1分
,
1分
椭圆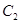 的半焦距
的半焦距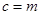 ,离心率
,离心率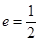 ,所以椭圆
,所以椭圆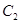 的长半轴长
的长半轴长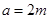 ,短半轴长
,短半轴长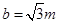 ,3分
,3分
所以椭圆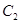 的方程为
的方程为 ,
4分
,
4分
当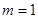 时,椭圆
时,椭圆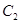 的方程
的方程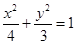 .
6分
.
6分
(2)假设存在满足条件的实数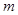
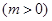 由
由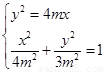 ,解得
,解得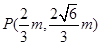 , 8分
, 8分
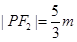 ,
,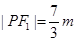 ,
,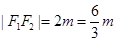 ,
11分
,
11分
所以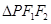 的三条边的边长分别是
的三条边的边长分别是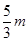 ,
,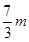 ,
,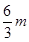
所以当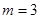 时使得
时使得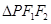 的三条边的边长是连续的自然数.
13分
的三条边的边长是连续的自然数.
13分
考点:1、抛物线和椭圆的方程及性质;2.存在性问题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=
如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=
 到点
到点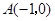 和
和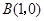 的距离分别为
的距离分别为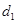 和
和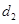 ,
, 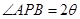 ,且存在常数
,且存在常数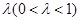 ,使得
,使得 .(如图所示)那么点
.(如图所示)那么点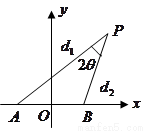
 的椭圆C2与抛物线C1在x轴上方的一个交点为P.
的椭圆C2与抛物线C1在x轴上方的一个交点为P.