题目内容
设f(x)=3ax2+2bx+c,若a+b+c=0,f(0)·f(1)>0.求证:(Ⅰ)方程f(x)=0有实根;
(Ⅱ)-2<![]() <-1;
<-1;
(Ⅲ)设x1,x2是方程f(x)=0的两个实根,则![]() ≤|x1-x2|<
≤|x1-x2|<![]() .
.
证明:(Ⅰ)若a=0,则b=-c,f(0)·f(1)=c(3a+2b+c)=-c2≤0与已知矛盾,∴a≠0,方程3ax2+2bx+c=0的判别式Δ=4(b2-3ac),由条件a+b+c=0,消去b得Δ=4(a2+c2-ac)=4[(a-![]() c)2+
c)2+![]() c2]>0.
c2]>0.
故方程f(x)=0有实根.
(Ⅱ)由f(0)·f(1)>0得,c(3a+2b+c)>0,由条件a+b+c=0消去C得(a+b)(2a+b)<0,因a2>0,∴(![]() +1)(
+1)(![]() +2)<0.
+2)<0.
故-2<![]() <-1.
<-1.
(Ⅲ)由条件知:x1+x2=-![]() ,x1-x2=
,x1-x2=![]() =-
=-![]() .
.
所以(x1-x2)2=(x1+x2)2-4x1x2=![]() (
(![]() +
+![]() )2+
)2+![]() ,
,
因为-2<![]() <-1,所以
<-1,所以![]() ≤(x1-x2)2<
≤(x1-x2)2<![]() ,
,
故![]() ≤|x1-x2|<
≤|x1-x2|<![]() .
.

练习册系列答案
相关题目
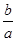 <-1
<-1