Question

设f(x)=3ax²+2bx+c，若a+b+c=0，f(0)>0，f(1)>0

求证：（1）a>0，－2<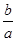<－1

（2）函数f(x)在（0，1）内有零点。

 

Answer 1

【答案】

见解析。

【解析】

试题分析：（1）∵f(0)>0,f(1)>0∴c>0,3a+2b+c>0再由a+b+c=0,消去b，得a>c>0；消去c，得a+b<0,2a+b>0。故－2<<－1；

（2）抛物线f(x)=3ax²+2bx+c的顶点坐标为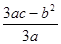（，）。∵－2<<－1

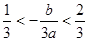∴。由于f()==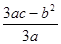=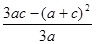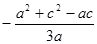<0而f(0)>0，f(1)>0，所以函数f(x)在（0，）和（，1）内各有一个零点

考点：主要考查一元二次不等式解法、二次函数图象和性质。

点评：综合性较强，涉及“二次”问题，借助于二次函数图象和性质分析，往往是必须地。