题目内容
(理科)对于函数f(x)=sinx,g(x)=cosx,h(x)=x+
,有如下四个命题:
(1)f(x)-g(x)的最大值为
;
(2)f[h(x)]在区间[-
,0]上是增函数;
(3)将f(x)的图象向右平移
个单位可得g(x)的图象.
(4)g[f(x)]是最小正周期为2π的周期函数.
其中真命题的序号是
| π |
| 3 |
(1)f(x)-g(x)的最大值为
| 2 |
(2)f[h(x)]在区间[-
| π |
| 2 |
(3)将f(x)的图象向右平移
| π |
| 2 |
(4)g[f(x)]是最小正周期为2π的周期函数.
其中真命题的序号是
(1)、(2)、(3)、(4)
(1)、(2)、(3)、(4)
.分析:根据两角和差的正弦公式,正弦函数的定义域和值域可得(1)正确. 根据f[h(x)]=sin(x+
),可得f[h(x)]在区间[-
,0]上是增函数,故(2)正确.
将f(x)的图象向右平移
个单位后得到函数y=sin(x-
)=g(x)的图象,故(3)正确. 由g[f(x)]=cos(sinx),最小正周期就是sinx的最小正周期2π,故(4)正确.
| π |
| 3 |
| π |
| 2 |
将f(x)的图象向右平移
| π |
| 2 |
| π |
| 2 |
解答:解:由于f(x)-g(x)=sinx-cosx=
sin(x-
),故它的最大值等于
,故(1)正确.
由于f[h(x)]=sin[(h(x)]=sin(x+
),当 x∈[-
,0]时,(x+
)∈[-
,
]?[-
,
],故f[h(x)]在区间[-
,0]上是增函数,故(2)正确.
将f(x)的图象向右平移
个单位后得到函数y=sin(x-
)=cosx=g(x)的图象,故(3)正确.
g[f(x)]=cos(f(x))=cos(sinx),它的最小正周期就是sinx的最小正周期为2π,故(4)正确.
故答案为:(1)、(2)、(3)、(4).
| 2 |
| π |
| 4 |
| 2 |
由于f[h(x)]=sin[(h(x)]=sin(x+
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
将f(x)的图象向右平移
| π |
| 2 |
| π |
| 2 |
g[f(x)]=cos(f(x))=cos(sinx),它的最小正周期就是sinx的最小正周期为2π,故(4)正确.
故答案为:(1)、(2)、(3)、(4).
点评:本题主要考查两角和差的正弦公式,正弦函数的定义域和值域、周期性、单调性,三角函数的图象平移,以及诱导公式的应用,属于中档题,掌握三角函数的图象性质,
是解题的关键.
是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,有如下四个命题:
,有如下四个命题: ;
; ,0]上是增函数;
,0]上是增函数;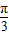 ,有如下四个命题:
,有如下四个命题: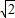 ;
;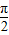 ,0]上是增函数;
,0]上是增函数;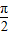 个单位可得g(x)的图象.
个单位可得g(x)的图象.