题目内容
已知函数 在
在 上是增函数,在
上是增函数,在 上为减函数.
上为减函数.
(1)求 的表达式;
的表达式;
(2)若当
 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的值;
的值;
(3)是否存在实数 使得关于
使得关于 的方程
的方程 在区间[0,2]上恰好有两个相异的实根,若存在,求实数
在区间[0,2]上恰好有两个相异的实根,若存在,求实数 的取值范围.
的取值范围.
(1)f(x)=(1+x)2-ln(1+x)2;(2)m>e2-2;(3)2-2ln2<b≤3-2ln3.
【解析】第一问中,利用f′(x)=2(1+x)-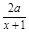 依题意f(x)在(-2,-1)上是增函数,在(-∞,-2)上为减函数.∴x=-2时,f(x)有极小值,∴f′(-2)=0.
依题意f(x)在(-2,-1)上是增函数,在(-∞,-2)上为减函数.∴x=-2时,f(x)有极小值,∴f′(-2)=0.
代入方程解得a=1,
故求得解析式
第二问中,当
 时,不等式
时,不等式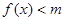 恒成立,只需要求解f(x)的最大值满足即可。第三问中,若存在实数b使得条件成立,方程f(x)=x2+x+b
恒成立,只需要求解f(x)的最大值满足即可。第三问中,若存在实数b使得条件成立,方程f(x)=x2+x+b
即为x-b+1-ln(1+x)2=0,构造函数令g(x)=x-b+1-ln(1+x)2,
求导得到结论。
解 (1)∵f′(x)=2(1+x)-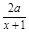 =2·
=2·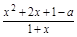 ,
,
依题意f(x)在(-2,-1)上是增函数,在(-∞,-2)上为减函数.∴x=-2时,f(x)有极小值,∴f′(-2)=0.代入方程解得a=1,故f(x)=(1+x)2-ln(1+x)2.
(2)由于f′(x)=2(1+x)-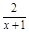 =
=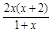 ,
,
令f′(x)=0,得x1=0,x2=-2.
(由于x∈ ,故x2=-2舍去),
,故x2=-2舍去),
易证函数在 上单调递减,
上单调递减,
在[0,e-1]上单调递增,
且f(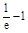 )=
)=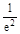 +2,f(e-1)=e2-2>
+2,f(e-1)=e2-2>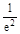 +2,
+2,
故当x∈ 时,f(x)max=e2-2,
时,f(x)max=e2-2,
因此若使原不等式恒成立只需m>e2-2即可.
(3)若存在实数b使得条件成立,
方程f(x)=x2+x+b,即为x-b+1-ln(1+x)2=0,
令g(x)=x-b+1-ln(1+x)2,
则g′(x)=1-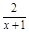 =
=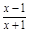 ,
,
令g′(x)>0,得x<-1或x>1,
令g′(x)<0,得-1<x<1,
故g(x)在[0,1]上单调递减,在[1,2]上单调递增,要使方程f(x)=x2+x+b在区间[0,2]上恰好有两个相异的实根,只需g(x)=0在区间[0,1]和[1,2]上各有一个实根,于是有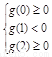
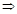 2-2ln2<b≤3-2ln3,
2-2ln2<b≤3-2ln3,
故存在这样的实数b,当2-2ln2<b≤3-2ln3时满足条件.

 在
在 上是增函数,
上是增函数, ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 在
在 上是增函数,则
上是增函数,则 的最小值是 ( )
的最小值是 ( )
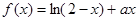 在
在 上是增函数,
上是增函数, 。当
。当 时,函数
时,函数 的最大值
的最大值 与最小值
与最小值 的差为
的差为 ,试求
,试求 的值。
的值。