题目内容
| |||||||||||
的实数，0＜a＜b．
答案：
解析：
解析：
(1) |
解析：由f(a)＝f(b)，得｜lga｜＝｜lgb｜．∵0＜a＜b，∴lga≠lgb，∴lga＝－lgb．∴lgab＝0，∴ab＝1． 又∵0＜a＜b，∴0＜a＜1＜b． |
(2) |
由f(b)＝2f ∴ ∴lgb＝2lg 点评：充分运用条件中隐含的等式“ab＝1”是证明此题的关键． |
，即｜lgb｜＝2
．∴0＜a＜1＜b，
＞
＝1，∴lgb＞0，lg
，化简为4b－b2＝a2＋2，∴0＜a＜1，∴2＜4b－b2＜3．
练习册系列答案
高中必刷题系列答案
相关题目
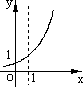
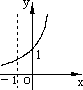
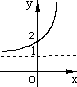
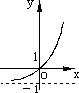
，试写出a与b的等量关系(至少写出两个)；
)，