题目内容
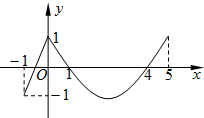 如图,定义在[-1,5]上的函数f(x)由一段线段和抛物线的一部分组成.
如图,定义在[-1,5]上的函数f(x)由一段线段和抛物线的一部分组成.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)指出函数f(x)的自变量x在什么范围内取值时,函数值大于0,小于0或等于0(不需说理由).
分析:(Ⅰ)利用待定系数法求函数f(x)的解析式;
(Ⅱ)根据函数的图象确定函数值对应的取值范围.
(Ⅱ)根据函数的图象确定函数值对应的取值范围.
解答:解:(Ⅰ)当-1≤x≤0时,直线过点(0,1)和(-1,-1),则对应的直线方程为f(x)=kx+1,
∵f(-1)=-k+1=-1,
∴k=2,即f(x)=2x+1,
当0≤x≤5时,抛物线与x轴的交点为(1,0)和(4,0),
∴设f(x)=a(x-1)(x-4),
∵f(0)=4a=1,
∴a=
,
即f(x)=
(x-1)(x-4),0≤x≤5.
(Ⅱ)由f(x)=2x+1=0,得x=-
,
∴当-
<x<1或4<x<5时,函数值大于0,
当-1<x<-
或1<x<4时,函数值小于0,
当x=-
或x=1或x=45时,函数值等于0.
∵f(-1)=-k+1=-1,
∴k=2,即f(x)=2x+1,
当0≤x≤5时,抛物线与x轴的交点为(1,0)和(4,0),
∴设f(x)=a(x-1)(x-4),
∵f(0)=4a=1,
∴a=
| 1 |
| 4 |
即f(x)=
| 1 |
| 4 |
(Ⅱ)由f(x)=2x+1=0,得x=-
| 1 |
| 2 |
∴当-
| 1 |
| 2 |
当-1<x<-
| 1 |
| 2 |
当x=-
| 1 |
| 2 |
点评:本题主要考查函数解析式的求法,利用待定系数法是解决本题的关键.

练习册系列答案
相关题目
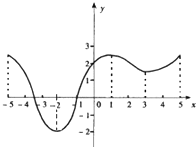 如图是定义在闭区间[-5,5]上的函数y=f(x)图象,该函数的单调增区间为( )
如图是定义在闭区间[-5,5]上的函数y=f(x)图象,该函数的单调增区间为( ) (2012•莆田模拟)如图是定义在[-4,6]上的函数f(x)的图象,若f(-2)=1,则不等式f(-x2+1)<1的解集是( )
(2012•莆田模拟)如图是定义在[-4,6]上的函数f(x)的图象,若f(-2)=1,则不等式f(-x2+1)<1的解集是( )