题目内容
(本小题满分12分)如图,四棱锥P--ABCD中,PB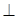 底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
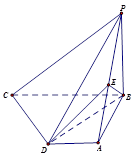
(1)求异面直线PA与CD所成的角;
(2)求证:PC∥平面EBD;
(3)求二面角A—BE--D的余弦值.
 底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
底面ABCD.底面ABCD为直角梯形,AD∥BC,AB=AD=PB=3,BC=6.点E在棱PA上,且PE=2EA.
(1)求异面直线PA与CD所成的角;
(2)求证:PC∥平面EBD;
(3)求二面角A—BE--D的余弦值.
(1)∠PAF=60°;(2)连结AC交BD于G,连结EG,由成比例线段得PC∥EG,
又EG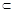 平面EBD,PC?平面EBD.∴PC∥平面EBD;
平面EBD,PC?平面EBD.∴PC∥平面EBD;
(3)二面角A-BE-D的余弦值为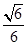 。
。
又EG
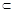 平面EBD,PC?平面EBD.∴PC∥平面EBD;
平面EBD,PC?平面EBD.∴PC∥平面EBD;(3)二面角A-BE-D的余弦值为
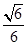 。
。试题分析:(1)∵PB⊥底面ABCD,在直角梯形ABCD中AB=AD=3,∴BC=6 取BC的中点F,连结AF,则AF∥CD.
∴异面直线PA和CD所成的角就是PA和AF所成的角∠PAF(或其补角),在△PAF中,AF=PA=PF=3
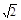 ,
,∴∠PAF=60° ………………3分
(2)连结AC交BD于G,连结EG,∵
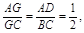 又
又 ∴
∴ ∴PC∥EG
∴PC∥EG又EG
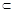 平面EBD,PC?平面EBD.∴PC∥平面EBD ……………7分
平面EBD,PC?平面EBD.∴PC∥平面EBD ……………7分(3)∵PB⊥平面ABCD,∴AD⊥PB.又∵AD⊥AB,∴AD⊥平面EAB.
作AH⊥BE,垂足为H,连结DH,则DH⊥BE,
∴∠AHD是二面角A-BE-D的平面角.在△ABE中,BE=
 AH=
AH=
∴tan∠AHD=
 , 所以,二面角A-BE-D的余弦值为
, 所以,二面角A-BE-D的余弦值为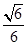 ……………12分
……………12分点评:典型题,立体几何中平行、垂直关系的证明及角的计算问题是高考中的必考题,注意遵循“一作、二证、三算”的解题步骤。

练习册系列答案
相关题目
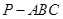 中,
中,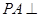 底面
底面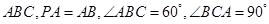 ,点
,点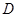 ,
,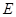 分别在棱
分别在棱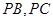 上,且
上,且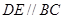
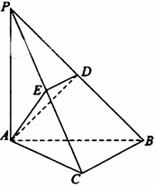
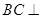 平面
平面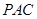 ;
;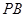 的中点时,求
的中点时,求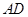 与平面
与平面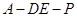 为直二面角?若存在,请确定点E的位置;若不存在,请说明理由.
为直二面角?若存在,请确定点E的位置;若不存在,请说明理由.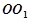 与三棱柱
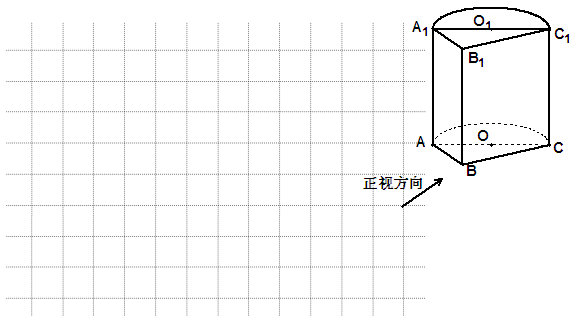
与三棱柱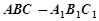 的组合体,其中,圆柱
的组合体,其中,圆柱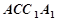 是边长为4的正方形,
是边长为4的正方形,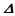
 为等腰直角三角形,
为等腰直角三角形,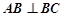 .
.
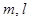 ,平面
,平面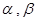 ,且
,且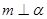 ,
,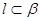 ,给出下列命题
,给出下列命题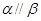 ,则
,则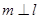 (2)若
(2)若 ,则
,则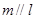
 中,
中, 点为棱
点为棱 的中点.
的中点.
 .
. ,求异面直线
,求异面直线 与
与 所成的角的余弦值.
所成的角的余弦值. 的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=
的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=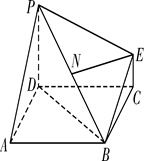
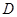 到平面
到平面 的距离.
的距离.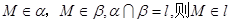 ;(4)空间中,相交于同一点的三条直线在同一平面内。
;(4)空间中,相交于同一点的三条直线在同一平面内。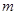 、
、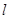 ,两个不同平面
,两个不同平面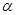 、
、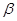 ,给出下列命题:
,给出下列命题: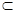
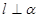 ,则
,则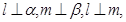 则
则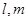 在平面
在平面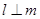 。
。