题目内容
设函数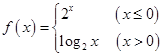 ,函数
,函数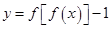 的零点个数为_________.
的零点个数为_________.
2
解析试题分析:当 时,
时,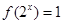 ,即
,即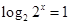 ,即
,即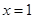 ;当
;当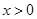 时,
时,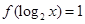 ,即
,即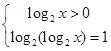 或
或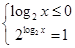 ,∴
,∴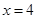 或
或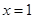 ,综上所得:
,综上所得: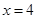 或
或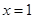 ,所以零点个数为2个.
,所以零点个数为2个.
考点:1.函数零点问题;2.对数、指数的运算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
设函数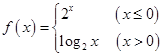 ,函数
,函数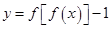 的零点个数为_________.
的零点个数为_________.
2
解析试题分析:当 时,
时,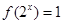 ,即
,即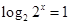 ,即
,即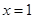 ;当
;当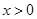 时,
时,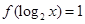 ,即
,即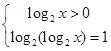 或
或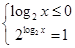 ,∴
,∴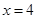 或
或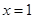 ,综上所得:
,综上所得: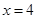 或
或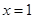 ,所以零点个数为2个.
,所以零点个数为2个.
考点:1.函数零点问题;2.对数、指数的运算.

 名校课堂系列答案
名校课堂系列答案