题目内容
已知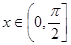 ,则函数
,则函数 的最小值为( )
的最小值为( )
| A.4 | B.5 | C.2 | D.3 |
B
解析试题分析:设 ,则
,则 ,当
,当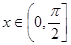 时,
时,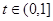 ,因为函数
,因为函数 在
在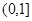 上单调递减,所以当
上单调递减,所以当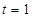 时,函数取得最小值,最小值为5.
时,函数取得最小值,最小值为5.
考点:本题考查的知识点是正弦函数的值域的求解方法,还考查了函数 的单调性的判断和值域的求解方法,本题的易错点在基本不等式的使用条件和等号能否成立的判断.
的单调性的判断和值域的求解方法,本题的易错点在基本不等式的使用条件和等号能否成立的判断.

练习册系列答案
相关题目
已知函数 的导函数为偶函数,则
的导函数为偶函数,则 ( )
( )
| A.0 | B.1 | C.2 | D.3 |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D. |
已知函数 的定义域为
的定义域为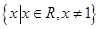 ,且
,且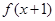 为奇函数,当
为奇函数,当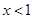 时,
时,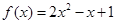 ,那么当
,那么当 时,
时, 的递减区间是( )
的递减区间是( )
A.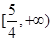 | B. | C.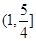 | D.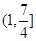 |
若函数 ,则函数
,则函数 ( )
( )
A.是奇函数,在 是增函数 是增函数 | B.是偶函数,在 是减函数 是减函数 |
C.是偶函数,在 是增函数 是增函数 | D.是奇函数,在 是减函数 是减函数 |
设函数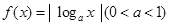 的定义域为
的定义域为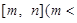
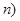 ,值域为
,值域为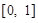 ,若
,若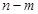 的最小值为
的最小值为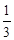 ,则实数a的值为( )
,则实数a的值为( )
A.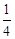 | B.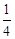 或 或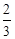 | C.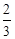 | D.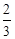 或 或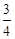 |
 图像上的任意一点
图像上的任意一点 的坐标
的坐标 满足条件
满足条件 ,则称函数
,则称函数 具有性质
具有性质 ,那么下列函数中具有性质
,那么下列函数中具有性质



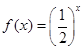 ,则函数
,则函数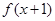 的反函数的图象可能是( )
的反函数的图象可能是( )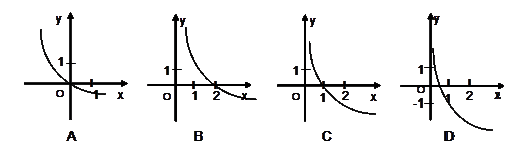
 ,
,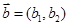 ,定义一运算:
,定义一运算: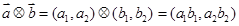 ,已知
,已知 ,
, .点Q在
.点Q在 的图像上运动,且满足
的图像上运动,且满足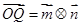 (其中O为坐标原点),则
(其中O为坐标原点),则