题目内容
设函数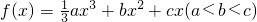 ,其图象在点A(1,f(1)),B(m,f(m))处的切线的斜率分别为0,-a.
,其图象在点A(1,f(1)),B(m,f(m))处的切线的斜率分别为0,-a.
(1)求证: ;
;
(2)若函数f(x)的递增区间为[s,t],求|s-t|的取值范围.
(1)证明:因为f′(x)=ax2+2bx+c…(1分)
于是依题意有f′(1)=a+2b+c=0,①…(1分)
f′(m)=am2+2bm+c=-a,②…(1分)
又由a<b<c,可得4a<a+2b+c<4c,即4a<0<4c,所以a<0,c>0,
由①得c=-a-2b,
∵a<b<c,a<0
∴ ③…(2分)
③…(2分)
将c=-a-2b代入②得am2+2bm-2b=0,即方程ax2+2bx-2b=0有实根,故其判别式△=4b2+8ab≥0,
由此可得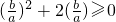 ,
,
解得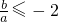 或
或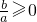 ④…(2分)
④…(2分)
由③、④即可得 ; …(1分)
; …(1分)
(2)解:由于f′(x)=ax2+2bx+c的判别式△′=4b2-4ac>0,…(1分)
所以方程a2+2bx+c=0(*)有两个不相等的实数根,设为x1,x2,
又由f′(1)=a+2b+c=0知1是(*)的一个根,记x1=1,…(1分)
则由根与系数的关系得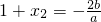 ,即
,即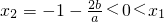 ,
,
当x<x2或x>1时,f'(x)>0;当x2<x<1时,f'(x)>0,…(1分)
所以函数f(x)的单调递增区间为[x2,1]
由题设[x2,1]=[s,t],…(1分)
因此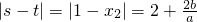 ,
,
由(1)知 ,所以|s-t|∈[2,4).…(1分)
,所以|s-t|∈[2,4).…(1分)
分析:(1)求导函数f′(x)=ax2+2bx+c,依题意有f′(1)=a+2b+c=0,f'(m)=am2+2bm+c=-a,结合a<b<c,即可得 ,将c=-a-2b代入f′(m)=am2+2bm+c=-a得am2+2bm-2b=0,即方程ax2+2bx-2b=0有实根,故其判别式△=4b2+8ab≥0,从而可得
,将c=-a-2b代入f′(m)=am2+2bm+c=-a得am2+2bm-2b=0,即方程ax2+2bx-2b=0有实根,故其判别式△=4b2+8ab≥0,从而可得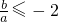 或
或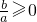 ,故问题得证;
,故问题得证;
(2)由于f'(x)=ax2+2bx+c的判别式△′=4b2-4ac>0,所以方程a2+2bx+c=0有两个不相等的实数根,设为x1,x2,
由于f′(1)=a+2b+c=0知1是(*)的一个根,记x1=1,利用根与系数的关系,可知函数f(x)的单调递增区间为[x2,1],从而[x2,1]=[s,t],进而可得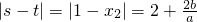 ,利用
,利用 ,可求|s-t|的范围.
,可求|s-t|的范围.
点评:本题考查的重点是导数知识的运用,考查不等式的证明,考查函数的单调性,同时考查了根与系数关系的运用,综合性强.
于是依题意有f′(1)=a+2b+c=0,①…(1分)
f′(m)=am2+2bm+c=-a,②…(1分)
又由a<b<c,可得4a<a+2b+c<4c,即4a<0<4c,所以a<0,c>0,
由①得c=-a-2b,
∵a<b<c,a<0
∴
 ③…(2分)
③…(2分)将c=-a-2b代入②得am2+2bm-2b=0,即方程ax2+2bx-2b=0有实根,故其判别式△=4b2+8ab≥0,
由此可得
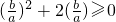 ,
,解得
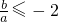 或
或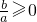 ④…(2分)
④…(2分)由③、④即可得
 ; …(1分)
; …(1分)(2)解:由于f′(x)=ax2+2bx+c的判别式△′=4b2-4ac>0,…(1分)
所以方程a2+2bx+c=0(*)有两个不相等的实数根,设为x1,x2,
又由f′(1)=a+2b+c=0知1是(*)的一个根,记x1=1,…(1分)
则由根与系数的关系得
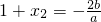 ,即
,即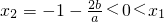 ,
,当x<x2或x>1时,f'(x)>0;当x2<x<1时,f'(x)>0,…(1分)
所以函数f(x)的单调递增区间为[x2,1]
由题设[x2,1]=[s,t],…(1分)
因此
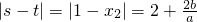 ,
,由(1)知
 ,所以|s-t|∈[2,4).…(1分)
,所以|s-t|∈[2,4).…(1分)分析:(1)求导函数f′(x)=ax2+2bx+c,依题意有f′(1)=a+2b+c=0,f'(m)=am2+2bm+c=-a,结合a<b<c,即可得
 ,将c=-a-2b代入f′(m)=am2+2bm+c=-a得am2+2bm-2b=0,即方程ax2+2bx-2b=0有实根,故其判别式△=4b2+8ab≥0,从而可得
,将c=-a-2b代入f′(m)=am2+2bm+c=-a得am2+2bm-2b=0,即方程ax2+2bx-2b=0有实根,故其判别式△=4b2+8ab≥0,从而可得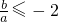 或
或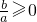 ,故问题得证;
,故问题得证;(2)由于f'(x)=ax2+2bx+c的判别式△′=4b2-4ac>0,所以方程a2+2bx+c=0有两个不相等的实数根,设为x1,x2,
由于f′(1)=a+2b+c=0知1是(*)的一个根,记x1=1,利用根与系数的关系,可知函数f(x)的单调递增区间为[x2,1],从而[x2,1]=[s,t],进而可得
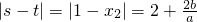 ,利用
,利用 ,可求|s-t|的范围.
,可求|s-t|的范围.点评:本题考查的重点是导数知识的运用,考查不等式的证明,考查函数的单调性,同时考查了根与系数关系的运用,综合性强.

练习册系列答案
相关题目
 ,其图象在点A(1,f(1)),B(m,f(m))处的切线的斜率分别为0,-a.
,其图象在点A(1,f(1)),B(m,f(m))处的切线的斜率分别为0,-a. ;
;