题目内容
本题14分)已知动圆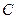 过点
过点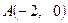 ,且与圆
,且与圆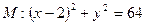 相内切.
相内切.
(1)求动圆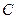 的圆心
的圆心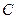 的轨迹方程;
的轨迹方程;
(2)设直线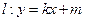 (其中
(其中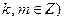 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点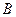 ,
,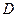 ,与双曲线
,与双曲线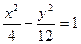 交于不同两点
交于不同两点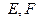 ,问是否存在直线
,问是否存在直线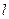 ,使得向量
,使得向量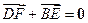 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
解:(1)圆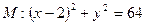 , 圆心
, 圆心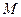 的坐标为
的坐标为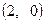 ,半径
,半径 .
.
∵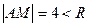 ,
,
∴点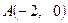 在圆
在圆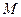 内.
内.
设动圆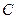 的半径为
的半径为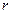 ,圆心为
,圆心为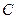 ,依题意得
,依题意得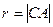 ,且
,且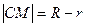 ,
,
即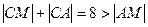 .
.
∴圆心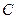 的轨迹是中心在原点,以
的轨迹是中心在原点,以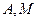 两点为焦点,长轴长为
两点为焦点,长轴长为 的椭圆,设其方程为
的椭圆,设其方程为 , 则
, 则 .
.
∴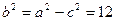 .
.
∴所求动圆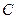 的圆心的轨迹方程为
的圆心的轨迹方程为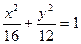 .
.
(2) 由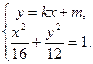 消去
消去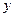 化简整理得:
化简整理得: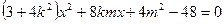 .
.
设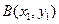 ,
,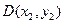 ,则
,则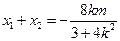 .
.
△
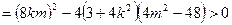 . ①
. ①
由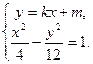 消去
消去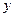 化简整理得:
化简整理得: .
.
设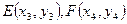 ,则
,则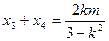 ,
,
△
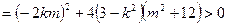 . ②
. ②
∵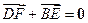 ,
,
∴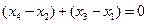 ,即
,即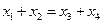 ,
,
∴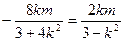 .
.
∴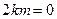 或
或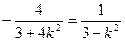 .
.
解得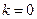 或
或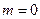 .
.
当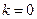 时,由①、②得
时,由①、②得 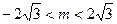 ,
,
∵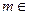 Z,
Z,
∴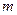 的值为
的值为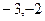
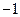 ,
,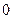 ,
,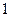
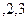 ;
;
当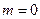 ,由①、②得
,由①、②得 解析

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 过点
过点 ,且与圆
,且与圆 相内切.
相内切.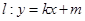 (其中
(其中 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点 ,
,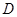 ,与双曲线
,与双曲线 交于不同两点
交于不同两点 ,问是否存在直线
,问是否存在直线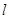 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. ,且与定直线
,且与定直线 相切.
相切. 的方程;
的方程; 是轨迹
是轨迹 、
、 为切点作轨迹
为切点作轨迹 ,证明:
,证明: .
. 相切,点C在
相切,点C在 上.
上. 的直线与曲线交于A、B两点.问直线
的直线与曲线交于A、B两点.问直线 是以
是以 为直角的直角三角形?如果存在,求出点C的坐标;若不能,请说明理由.
为直角的直角三角形?如果存在,求出点C的坐标;若不能,请说明理由.