题目内容
设x,y满足
,则z=x+y( )
|
| A、有最小值2,最大值3 |
| B、有最小值2,无最大值 |
| C、有最大值3,无最小值 |
| D、既无最小值,也无最大值 |
分析:本题考查的知识点简单线性规划问题,我们先在坐标系中画出满足约束条件
对应的平面区域,根据目标函数z=x+y及直线2x+y=4的斜率的关系,即可得到结论.
|
解答:解析:如图作出不等式组表示
的可行域,如下图所示:
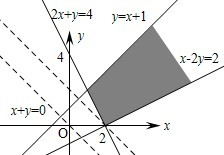
由于z=x+y的斜率大于2x+y=4的斜率,
因此当z=x+y过点(2,0)时,z有最小值,
但z没有最大值.
故选B
|

由于z=x+y的斜率大于2x+y=4的斜率,
因此当z=x+y过点(2,0)时,z有最小值,
但z没有最大值.
故选B
点评:目判断标函数的有元最优解,处理方法一般是:①将目标函数的解析式进行变形,化成斜截式②分析Z与截距的关系,是符号相同,还是相反③根据分析结果,结合图形做出结论④根据目标函数斜率与边界线斜率之间的关系分析,即可得到答案.

练习册系列答案
相关题目