题目内容
已知函数 (其中常数a,b∈R),
(其中常数a,b∈R), .
.(Ⅰ)当a=1时,若函数f(x)是奇函数,求f(x)的极值点;
(Ⅱ)若a≠0,求函数f(x)的单调递增区间;
(Ⅲ)当
 时,求函数g(x)在[0,a]上的最小值h(a),并探索:是否存在满足条件的实数a,使得对任意的x∈R,f(x)>h(a)恒成立.
时,求函数g(x)在[0,a]上的最小值h(a),并探索:是否存在满足条件的实数a,使得对任意的x∈R,f(x)>h(a)恒成立.
【答案】分析:(I)根据所给的函数是一个奇函数,写出奇函数成立的等式,整理出b的值是0,得到函数的解析式,对函数求导,使得导函数等于0,求出极值点.
(II)要求函数的单调增区间,首先对函数求导,使得导函数大于0,解不等式,问题转化为解一元二次不等式,注意对于a值进行讨论.
(Ⅲ)求出函数g(x)在[0,a]上的极值、端点值,比较其中最小者即为h(a),再利用奇函数性质及基本不等式求出f(x)的最小值,对任意的x∈R,f(x)>h(a)恒成立,
等价于f(x)min>h(a),在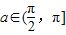 上只要找到一a值满足该不等式即可.
上只要找到一a值满足该不等式即可.
解答:解:(Ⅰ)当a=1时,
因为函数f(x)是奇函数,∴对x∈R,f(-x)=-f(x)成立,
得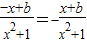 ,∴
,∴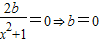 ,
,
∴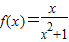 ,得
,得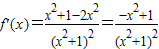 ,
,
令f'(x)=0,得x2=1,∴x=±1,
经检验x=±1是函数f(x)的极值点.
(Ⅱ)因为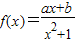 ,∴
,∴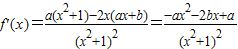 ,
,
令f'(x)>0⇒-ax2-2bx+a>0,得ax2+2bx-a<0,
①当a>0时,方程ax2+2bx-a=0的判别式△=4b2+4a2>0,两根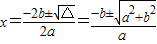 ,
,
单调递增区间为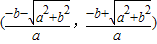 ,
,
②当a<0时,单调递增区间为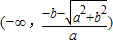 和
和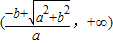 .
.
(Ⅲ) 因为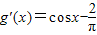 ,当x∈[0,a]时,令g'(x)=0,得
,当x∈[0,a]时,令g'(x)=0,得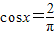 ,其中
,其中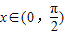 .
.
当x变化时,g'(x)与g(x)的变化情况如下表:
∴函数g(x)在[0,a]上的最小值为g(0)与g(a)中的较小者.
又g(0)=0,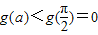 ,∴h(a)=g(a),∴
,∴h(a)=g(a),∴ ,
,
b=0时,由函数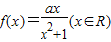 是奇函数,且
是奇函数,且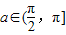 ,
,
∴x>0时,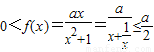 ,当x=1时取得最大值
,当x=1时取得最大值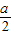 ;
;
当x=0时,f(0)=0;当x<0时,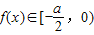 ,
,
∴函数f(x)的最小值为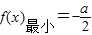 ,
,
要使对任意x∈R,f(x)>h(a)恒成立,则f(x)最小>h(a),
∴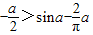 ,即不等式
,即不等式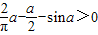 在
在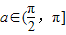 上有解,a=π符合上述不等式,
上有解,a=π符合上述不等式,
∴存在满足条件的实数a=π,使对任意x∈R,f(x)>h(a)恒成立.
点评:本题是考查导数的综合应用的题目,是一个以考查函数的单调性和最值为主的题目,同时考查分析问题解决问题的能力,解题过程中要解含参数的一元二次不等式的解法.
(II)要求函数的单调增区间,首先对函数求导,使得导函数大于0,解不等式,问题转化为解一元二次不等式,注意对于a值进行讨论.
(Ⅲ)求出函数g(x)在[0,a]上的极值、端点值,比较其中最小者即为h(a),再利用奇函数性质及基本不等式求出f(x)的最小值,对任意的x∈R,f(x)>h(a)恒成立,
等价于f(x)min>h(a),在
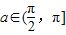 上只要找到一a值满足该不等式即可.
上只要找到一a值满足该不等式即可.解答:解:(Ⅰ)当a=1时,
因为函数f(x)是奇函数,∴对x∈R,f(-x)=-f(x)成立,
得
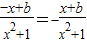 ,∴
,∴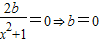 ,
,∴
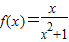 ,得
,得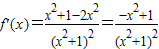 ,
,令f'(x)=0,得x2=1,∴x=±1,
经检验x=±1是函数f(x)的极值点.
(Ⅱ)因为
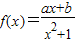 ,∴
,∴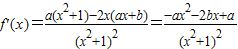 ,
,令f'(x)>0⇒-ax2-2bx+a>0,得ax2+2bx-a<0,
①当a>0时,方程ax2+2bx-a=0的判别式△=4b2+4a2>0,两根
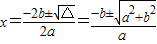 ,
,单调递增区间为
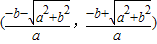 ,
,②当a<0时,单调递增区间为
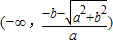 和
和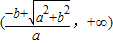 .
.(Ⅲ) 因为
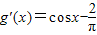 ,当x∈[0,a]时,令g'(x)=0,得
,当x∈[0,a]时,令g'(x)=0,得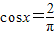 ,其中
,其中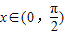 .
.当x变化时,g'(x)与g(x)的变化情况如下表:
| x | (0,x) | x | (x,a) |
| g'(x) | + | - | |
| g(x) | ↗ | ↘ |
又g(0)=0,
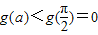 ,∴h(a)=g(a),∴
,∴h(a)=g(a),∴ ,
,b=0时,由函数
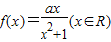 是奇函数,且
是奇函数,且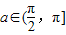 ,
,∴x>0时,
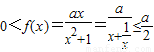 ,当x=1时取得最大值
,当x=1时取得最大值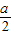 ;
;当x=0时,f(0)=0;当x<0时,
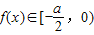 ,
,∴函数f(x)的最小值为
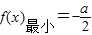 ,
,要使对任意x∈R,f(x)>h(a)恒成立,则f(x)最小>h(a),
∴
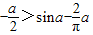 ,即不等式
,即不等式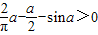 在
在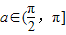 上有解,a=π符合上述不等式,
上有解,a=π符合上述不等式,∴存在满足条件的实数a=π,使对任意x∈R,f(x)>h(a)恒成立.
点评:本题是考查导数的综合应用的题目,是一个以考查函数的单调性和最值为主的题目,同时考查分析问题解决问题的能力,解题过程中要解含参数的一元二次不等式的解法.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
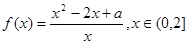 ,其中常数a > 0.
,其中常数a > 0. 上是减函数;
上是减函数;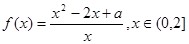 ,其中常数a > 0.
,其中常数a > 0. 上是减函数;
上是减函数;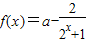 (其中常数a∈R)
(其中常数a∈R)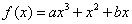 (其中常数a,b∈R),
(其中常数a,b∈R),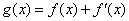 是奇函数.
是奇函数. 的表达式;
的表达式; 的单调性,并求
的单调性,并求