题目内容
对一批产品的长度(单位: mm)进行抽样检测, 下图喂检测结果的频率分布直方图. 根据标准, 产品长度在区间[20,25)上的为一等品, 在区间[15,20)和区间[25,30)上的为二等品, 在区间[10,15)和[30,35)上的为三等品. 用频率估计概率, 现从该批产品中随机抽取一件, 则其为二等品的概率为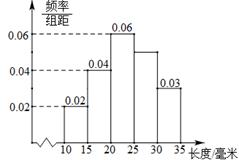
| A.0.09 | B.0.20 | C.0.25 | D.0.45 |
D
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2014年3月,为了调查教师对十二届全国人民代表大会二次会议的了解程度,黄冈市拟采用分层抽样的方法从A,B,C三所不同的中学抽取60名教师进行调查,已知A,B,C三所中学分别有180,270,90名教师,则从C学校学校中抽取的人数是( )
| A.10 | B.12 | C.18 | D.24 |
某单位随机统计了某4天的用电量(度)与当天气温(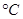 )如下表,以了解二者的关系。
)如下表,以了解二者的关系。
气温(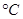 ) ) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
由表中数据得回归直线方程
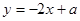 ,则
,则
A.60 B.58 C.40 D.以上都不对
没有信息损失的统计图表是 ( )
| A.条形统计图 | B.扇形统计图 | C.折线统计图 | D.茎叶图 |
已知 的取值如下表:
的取值如下表: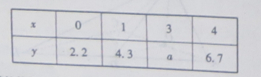
根据上表提供的数据,求出y对x的线性回归方程为 ,则表中的数据a的值为( )
,则表中的数据a的值为( )
| A.4.6 | B.4.8 | C.5.45 | D.5.55 |
(2013•重庆)如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为( )
| A.0.2 | B.0.4 | C.0.5 | D.0.6 |
实验测得四组(x,y)的值为(1,2),(2,3),(3,4),(4,5),则y与x之间的回归直线方程为( )
A.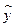 =x+1 =x+1 | B.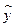 =x+2 =x+2 |
C.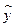 =2x+1 =2x+1 | D.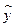 =2x+2 =2x+2 |
一台机器由于使用时间较长,但还可以使用,它按不同的转速生产出来的某机器零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,下表是抽样试验结果:
| 转速x/(rad/s) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y/件 | 11 | 9 | 8 | 5 |
A.10转/s以下
B.15转/s以下
C.20转/s以下
D.25转/s以下