题目内容
已知数列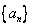 满足
满足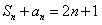 。
。
(1)写出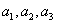 ,并推测
,并推测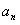 的表达式;
的表达式;
(2)用数学归纳法证明所得的结论。
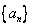 满足
满足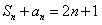 。
。(1)写出
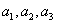 ,并推测
,并推测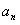 的表达式;
的表达式; (2)用数学归纳法证明所得的结论。
解:(1)a1=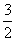 ,a2=
,a2=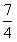 ,a3=
,a3=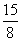 ,
,
猜想an=2-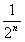 。
。
(2)①由(1)已得当n=1时,命题成立;
②假设n=k时,命题成立,即 ak=2-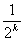 ,
,
当n=k+1时,a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,
且a1+a2+……+ak=2k+1-ak,
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-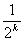 ,ak+1=2-
,ak+1=2-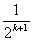 ,
,
即当n=k+1时,命题成立,
根据①②得n∈N*,an=2-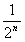 都成立。
都成立。
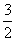 ,a2=
,a2=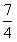 ,a3=
,a3=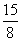 ,
, 猜想an=2-
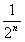 。
。(2)①由(1)已得当n=1时,命题成立;
②假设n=k时,命题成立,即 ak=2-
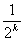 ,
,当n=k+1时,a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,
且a1+a2+……+ak=2k+1-ak,
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-
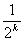 ,ak+1=2-
,ak+1=2-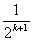 ,
, 即当n=k+1时,命题成立,
根据①②得n∈N*,an=2-
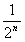 都成立。
都成立。 
练习册系列答案
相关题目
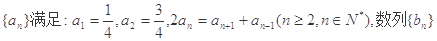 满足:
满足: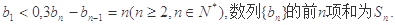
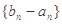 为等比数列;
为等比数列;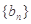 为递增数列;
为递增数列; 的取值范围。
的取值范围。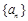 满足
满足 .
.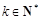 ,是否存在
,是否存在 (
(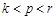 )使
)使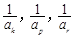 成等差数列?若存
成等差数列?若存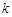 分别表示
分别表示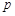 和
和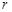 (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;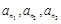 .
. 满足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0
满足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0 的表达式,并用数学归纳法证明你的结论
的表达式,并用数学归纳法证明你的结论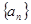 满足
满足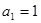 ,
,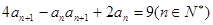
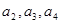 。(2)由(1)猜想
。(2)由(1)猜想