题目内容
已知数列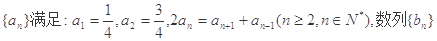 满足:
满足: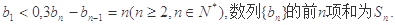
(1)求证:数列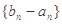 为等比数列;
为等比数列;
(2)求证:数列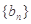 为递增数列;
为递增数列;
(3)若当且仅当 的取值范围。
的取值范围。
【答案】
(I)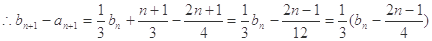
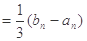 ,
,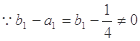 ,
, 为首项,以
为首项,以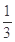 为公比的等比数列;
为公比的等比数列;
(II)
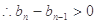 ,
,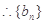 是单调递增数列;
是单调递增数列;
(III)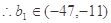 。
。
【解析】
试题分析:(I)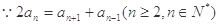
 是等差数列
是等差数列
又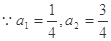
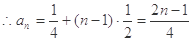 2分
2分
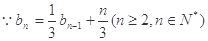
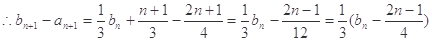
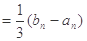 5分
5分
又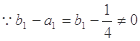
 为首项,以
为首项,以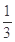 为公比的等比数列
6分
为公比的等比数列
6分
(II)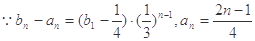
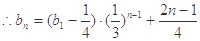
当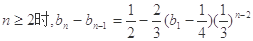
又
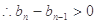
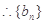 是单调递增数列
9分
是单调递增数列
9分
(III) 时,
时,
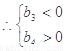 10分
10分
即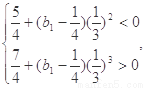 12分
12分
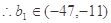 13分
13分
考点:本题主要考查数列的递推关系,等差数列、等比数列的证明,等比数列的求和,不等式组解法。
点评:典型题,本题在考查等差数列、等比数列基础知识的同时,有意给出递推关系,增大试题难度,同时通过前n项和最值的讨论,和不等式组解法结合在一起,具有一定综合性。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
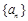 满足
满足 .
.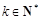 ,是否存在
,是否存在 (
(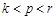 )使
)使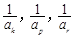 成等差数列?若存
成等差数列?若存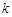 分别表示
分别表示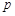 和
和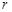 (只要写出一组);若不存在,请说明理由;
(只要写出一组);若不存在,请说明理由;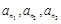 .
. 满足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0
满足a1=1,an+1>an,且(an+1-an)2-2(an+1+an)+1=0 的表达式,并用数学归纳法证明你的结论
的表达式,并用数学归纳法证明你的结论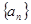 满足
满足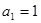 ,
,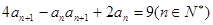
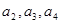 。(2)由(1)猜想
。(2)由(1)猜想