题目内容
已知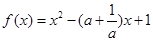 .
.
当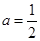 时,解不等式
时,解不等式 ;
;
(2)若 ,解关于
,解关于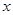 的不等式
的不等式 .
.
(1)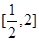 ;(2)当
;(2)当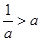 时,不等式的解集为
时,不等式的解集为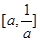 ;当
;当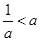 时,不等式的解集为
时,不等式的解集为 ;
;
当 时,等式的解集为
时,等式的解集为 .
.
解析试题分析:(1)当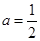 ,
, ,令
,令 ,则
,则 ,则由一元二次不等式与二次函数及一元二次方程三者之间的关系可知,不等式的解集为
,则由一元二次不等式与二次函数及一元二次方程三者之间的关系可知,不等式的解集为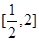 ;(2)一元二次方程
;(2)一元二次方程 的两根为
的两根为 ,根据一元二次不等式与一元二次方程之间的关系可知,需对
,根据一元二次不等式与一元二次方程之间的关系可知,需对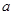 与
与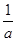 的大小关系分以下三种情况讨论:当
的大小关系分以下三种情况讨论:当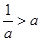 时,不等式的解集为
时,不等式的解集为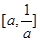 ;当
;当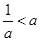 时,不等式的解集为
时,不等式的解集为 ;当
;当 时,不等式的解集为
时,不等式的解集为 .
.
试题解析:(1)当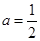 时,有不等式
时,有不等式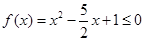 , 2分
, 2分
∴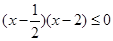 ,∴不等式的解集为
,∴不等式的解集为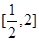 ; 4分
; 4分
(2)∵不等式 ,一元二次方程
,一元二次方程 ,两根为
,两根为 ,
,
∴当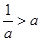 时,有
时,有 ,∴不等式的解集为
,∴不等式的解集为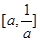 ; 7分
; 7分
当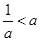 时,有
时,有 ,∴不等式的解集为
,∴不等式的解集为 ; 10分
; 10分
当 时,有
时,有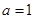 ,∴不等式的解集为
,∴不等式的解集为 . 12分
. 12分
考点:1.一元二次不等式、二次函数、一元二次方程三个二次之间的关系;2.分类讨论的数学思想.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
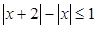 的解集为__
的解集为__ 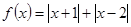 的最小值为
的最小值为 .
.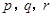 为正实数,且
为正实数,且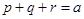 ,求证:
,求证: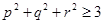 .
.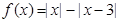
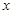 的不等式
的不等式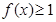 ;
;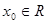 ,使得
,使得 成立,求实数
成立,求实数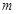 的取值范围.
的取值范围.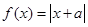 .
.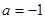 时,求不等式
时,求不等式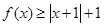 的解集;
的解集;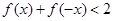 存在实数解,求实数
存在实数解,求实数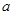 的取值范围.
的取值范围.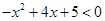 ;
;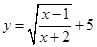 .
.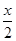 +1.
+1.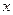 的两个不等式
的两个不等式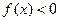 和
和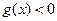 的解集分别为
的解集分别为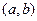 和
和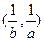 ,则称这两个不等式为对偶不等式。如果不等式
,则称这两个不等式为对偶不等式。如果不等式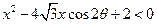 与不等式
与不等式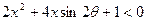 为对偶不等式,且
为对偶不等式,且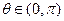 ,则
,则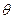 =_______________
=_______________