题目内容
设椭圆C: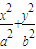 =1(a>b>0)的左、右焦点分别为F1、F2,离心率为
=1(a>b>0)的左、右焦点分别为F1、F2,离心率为 ,左焦点F1到直线l:
,左焦点F1到直线l: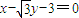 的距离等于长半轴长.
的距离等于长半轴长.(I)求椭圆C的方程;
(II)过右焦点F2作斜率为k的直线l与椭圆C交于M、N两点,线段MN的中垂线与x轴相交于点P(m,O),求实数m的取值范围.
【答案】分析:(I)由离心率为 得
得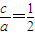 ,所以F1(-
,所以F1(- a,0),由F1到直线l的距离为a,所以
a,0),由F1到直线l的距离为a,所以 解得a,从而得c,由b2=a2-c2得b;
解得a,从而得c,由b2=a2-c2得b;
(II)由(I)知F2(1,0),设直线l的方程为:y=k(x-1),与椭圆方程联立消掉y得x的二次方程,易知恒有△>0,设M(x1,y1),N(x2,y2),根据韦达定理及中点坐标公式可得MN中点的坐标,分情况讨论:当k=0时易求m值;当k≠0时写出MN中垂线方程,令y=0得m,变形后用基本函数的范围即可求得m的范围,综合两种情况即可求得m的取值范围;
解答:解:(I)由已知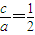 ,可得F1(-
,可得F1(- a,0),
a,0),
由F1到直线l的距离为a,所以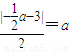 ,
,
解得a=2,所以c=1,b2=a2-c2=3,得b=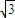 ,
,
所以所求椭圆C的方程为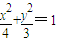 ;
;
(II)由(I)知F2(1,0),设直线l的方程为:y=k(x-1),
由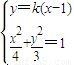 消去y得(3+4k2)x2-8k2x+4k2-12=0,
消去y得(3+4k2)x2-8k2x+4k2-12=0,
因为l过点F2,所以△>0恒成立,
设M(x1,y1),N(x2,y2),
则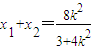 ,y1+y2=k(x1+x2-2)=
,y1+y2=k(x1+x2-2)=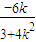 ,
,
所以MN中点(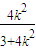 ,
,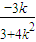 ),
),
当k=0时,MN为长轴,中点为原点,则m=0,
当k≠0时MN中垂线方程为y+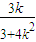 =-
=-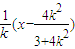 ,
,
令y=0,得m=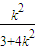 =
=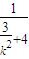 ,
,
因为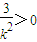 ,所以
,所以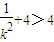 ,可得0<m<
,可得0<m< ,
,
综上可知实数m的取值范围是[0, ).
).
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查分析解决问题的能力,解决该类题目常用的知识为韦达定理、判别式等,应熟练掌握.
 得
得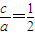 ,所以F1(-
,所以F1(- a,0),由F1到直线l的距离为a,所以
a,0),由F1到直线l的距离为a,所以 解得a,从而得c,由b2=a2-c2得b;
解得a,从而得c,由b2=a2-c2得b;(II)由(I)知F2(1,0),设直线l的方程为:y=k(x-1),与椭圆方程联立消掉y得x的二次方程,易知恒有△>0,设M(x1,y1),N(x2,y2),根据韦达定理及中点坐标公式可得MN中点的坐标,分情况讨论:当k=0时易求m值;当k≠0时写出MN中垂线方程,令y=0得m,变形后用基本函数的范围即可求得m的范围,综合两种情况即可求得m的取值范围;
解答:解:(I)由已知
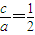 ,可得F1(-
,可得F1(- a,0),
a,0),由F1到直线l的距离为a,所以
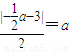 ,
,解得a=2,所以c=1,b2=a2-c2=3,得b=
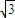 ,
,所以所求椭圆C的方程为
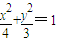 ;
;(II)由(I)知F2(1,0),设直线l的方程为:y=k(x-1),
由
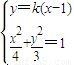 消去y得(3+4k2)x2-8k2x+4k2-12=0,
消去y得(3+4k2)x2-8k2x+4k2-12=0,因为l过点F2,所以△>0恒成立,
设M(x1,y1),N(x2,y2),
则
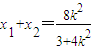 ,y1+y2=k(x1+x2-2)=
,y1+y2=k(x1+x2-2)=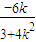 ,
,所以MN中点(
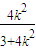 ,
,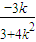 ),
),当k=0时,MN为长轴,中点为原点,则m=0,
当k≠0时MN中垂线方程为y+
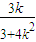 =-
=-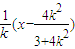 ,
,令y=0,得m=
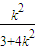 =
=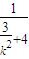 ,
,因为
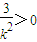 ,所以
,所以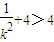 ,可得0<m<
,可得0<m< ,
,综上可知实数m的取值范围是[0,
 ).
).点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查分析解决问题的能力,解决该类题目常用的知识为韦达定理、判别式等,应熟练掌握.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 +
+ =1(a>b>0)的左焦点为F1=(-
=1(a>b>0)的左焦点为F1=(- ,0),椭圆过点P(-
,0),椭圆过点P(- ,
, )
) =1(a>b>0)的左、右焦点分别为F1、F2,离心率为
=1(a>b>0)的左、右焦点分别为F1、F2,离心率为 ,左焦点F1到直线l:
,左焦点F1到直线l: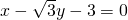 的距离等于长半轴长.
的距离等于长半轴长. +
+ =1(a>b>0)过点M(1,1),离心率e=
=1(a>b>0)过点M(1,1),离心率e= ,O为坐标原点.
,O为坐标原点. •
• 为定值.
为定值. 设椭圆C:
设椭圆C: +
+ =1(a>b>0)的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
=1(a>b>0)的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且 =
=
 .
. y+3=0相切,求椭圆C的方程.
y+3=0相切,求椭圆C的方程. +
+ =1(a>b>0)的左焦点为F1=(-
=1(a>b>0)的左焦点为F1=(- ,0),椭圆过点P(-
,0),椭圆过点P(- ,
, )
)