题目内容
已知圆的直角坐标方程为x2+y2-2x=0.在以原点为极点,x轴非负半轴为极轴的极坐标系中,该圆的方程为( )
分析:先根据圆的标准方程得出其在新的直角坐标系下的圆的方程,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得圆的极坐标方程.
解答:解:在以原来的原点为原点,原来的x轴非负半轴为新x轴的直角坐标系中,圆的直角坐标方程为x2+y2+2x=0.
利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换,
圆的直角坐标方程为x2+y2+2x=0,所以ρ2+2ρcosθ=0,即ρ=-2cosθ.
故选C.
利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换,
圆的直角坐标方程为x2+y2+2x=0,所以ρ2+2ρcosθ=0,即ρ=-2cosθ.
故选C.
点评:本题考查圆的极坐标方程求解,用到了转化代换法.属于基础题,注意基本方法的运用.

练习册系列答案
相关题目
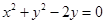 .在以原点为极点,
.在以原点为极点, 轴正半轴为极轴的极坐标系中,该圆的方程为(
)
轴正半轴为极轴的极坐标系中,该圆的方程为(
)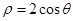 B、
B、 C、
C、 D、
D、