题目内容
已知函数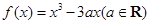
，若直线
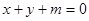对任意的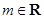
都不是曲线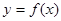
的切线，则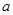
的取值范围是 ．
【答案】
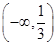
【解析】
试题分析：首先分析对任意的m直线
都不是曲线y=f（x）的切线的含义，即可求出函数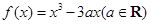
的导函数，使直线与其不相交即可．解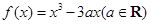：，则f（x）′=3x2-3a，若直线任意的m∈R都不是曲线y=f（x）的切线，则直线的斜率为-1，f（x）′=3x2-3a与直线没有交点，又抛物线开口向上则必在直线上面，即最小值大于直线斜率，则当x=0时取最大值，-3a＞-1，则a的取值范围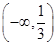为，故答案为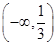
考点：函数与方程
点评：此题只要考查函数与方程的综合应用，以及函数导函数的计算，属于综合性问题，计算量小但有一定的难度，属于中等题
练习册系列答案
相关题目
[番茄花园1] 本题共有3个小题，第1小题满分3分，第2小题满分5分，第3小题满分10分。
若实数
、
、
满足
，则称比远离.
（1）若
比1远离0，求的取值范围；
（2）对任意两个不相等的正数
、
，证明：
比
远离
；
（3）已知函数
的定义域
.任取
，等于
和
中远离0的那个值.写出函数的解析式，并指出它的基本性质（结论不要求证明）.
23本题共有3个小题，第1小题满分3分，第2小题满分6分，第3小题满分9分.
已知椭圆
的方程为
，点P的坐标为（-a，b）.
（1）若直角坐标平面上的点M、A(0,-b)，B(a，0)满足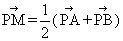
,求点
的坐标；
（2）设直线
交椭圆于
、
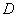两点，交直线
于点
.若
，证明：为
的中点；
（3）对于椭圆上的点Q（a cosθ，b sinθ）（0＜θ＜π），如果椭圆上存在不同的两个交点
、
满足
,写出求作点、的步骤，并求出使、存在的θ的取值范围.
[番茄花园1]22.