题目内容
4.若两个非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则$\overrightarrow{a}$所在的直线与$\overrightarrow{b}$所在直线的夹角为( )| A. | θ | B. | π-θ | C. | θ或π-θ | D. | 与θ无关 |
分析 由直线的夹角和向量夹角的关系可得.
解答 解:∵两个非零向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,
∴当θ为0或锐角时,$\overrightarrow{a}$所在的直线与$\overrightarrow{b}$所在直线的夹角为θ;
当θ为钝角或平角时,$\overrightarrow{a}$所在的直线与$\overrightarrow{b}$所在直线的夹角为π-θ;
故选:C
点评 本题考查向量的夹角和直线的夹角的关系,属基础题.

练习册系列答案
相关题目
9.各项均为正数的数列{an}满足:na2n+1=(n+1)a2n+anan+1,且a3=$\frac{3π}{4}$,若Sn为数列{an}的前n项和,则tanS2015等于( )
| A. | -$\sqrt{3}$ | B. | -1 | C. | 0 | D. | 1 |
14.若logax=l,logay=m,logaz=n,则用l、m、n表示loga$\frac{{x}^{3}}{{y}^{2}{z}^{\frac{1}{3}}}$所得的结果是( )
| A. | 3l-2m+$\frac{1}{3}n$ | B. | 3l-2m-$\frac{1}{3}n$ | C. | 3l-2m+3n | D. | 3l-2m-3n |
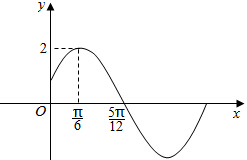 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.