题目内容

在△ABC中，点O是其内一点，若
OA
+
OB
+
OC
=
0
，且
OA
•
OB
=
OB
•
OC
=
OC
•
OA
，则△ABC的形状是（　　）
分析：设AB的中点为D，由
OA
+
OB
+
OC
=
0
，可得 O为△ABC的重心．由
OA
•
OB
=
OB
•
OC
=
OC
•
OA
，可得O为△ABC的垂心，由此可得，△ABC的形状．
解答：解：设AB的中点为D，∵
OA
+
OB
+
OC
=
0
，∴2
OD
=-
OC
，∴2|
OD
|=|
OC
|，
∴O为△ABC的重心．
∵
OA
•
OB
=
OB
•
OC
=
OC
•
OA
，∴
OB
•(
OA
-
OC
)=0，即
OB
•
CA
=0，
∴
OB
⊥
CA
．
 同理可证，
OA
⊥
CB
，
OC
⊥
BA
，故O为△ABC的垂心．
 综上可得，△ABC的形状是等边三角形，
 故选B．
点评：本题考查三角形的重心、垂心的定义，等边三角形的性质，判断O为△ABC的重心是解题的难点，属于中档题．
练习册系列答案
相关题目
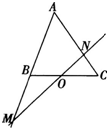精英家教网如图，在△ABC中，点O是BC的中点．过点O的直线分别交直线AB、AC于不同的两点M、N，若
AB
=m
AM
，
AC
=n
AN
，则m+n的值为
 
．
在△ABC中，点O是BC的中点，过点O的直线分别交直线AB，AC与不同的两点M，N，若
AB
=m
AM
，
AC
=n
AN
，m＞0，n＞0，则
1
m
+
4
n
的最小值为（　　）
在△ABC中，点O是BC的中点，过点O的直线分别交直线AB、AC于不同的两点M、N，若
AB
=m
AM
，
AC
=n
AN
，则mn的最大值为
1
1
．
如图，在△ABC中，点O是BC的中点，过点O的直线分别交直线AB，AC于不同的两点M，N，若
AB
=m
AM
，
AC
=n
AN
，求m+n的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网