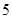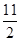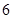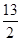题目内容
(本题满分14分)
等比数列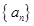 中,
中,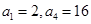 ,
,
(1)求数列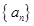 的通项公式;
的通项公式;
(2)若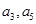 分别是等差数列
分别是等差数列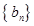 的第3项和第5项,求数列
的第3项和第5项,求数列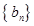 的通项公式及前n项和
的通项公式及前n项和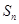 .
.
等比数列
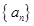 中,
中,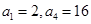 ,
, (1)求数列
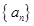 的通项公式;
的通项公式; (2)若
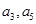 分别是等差数列
分别是等差数列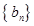 的第3项和第5项,求数列
的第3项和第5项,求数列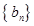 的通项公式及前n项和
的通项公式及前n项和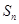 .
.(1)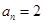
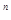 ;(2)
;(2)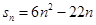 .
.
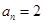
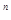 ;(2)
;(2)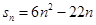 .
.第一问利用设数列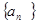 的公比为
的公比为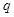 , ∴
, ∴ 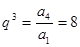
∴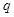 =2, ∴
=2, ∴ 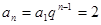
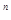
第二问由(1)得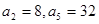 , ∴
, ∴ 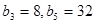
设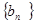 的公差为d, ∴
的公差为d, ∴ 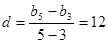
∴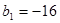 ∴
∴ 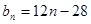 得到和式。
得到和式。
解:设数列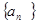 的公比为
的公比为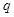 , ∴
, ∴ 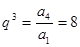 ·……………………3分
·……………………3分
∴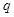 =2, ∴
=2, ∴ 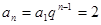
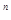 ……………………7分
……………………7分
(2)由(1)得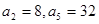 , ∴
, ∴ 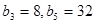
设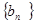 的公差为d, ∴
的公差为d, ∴ 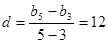 …………………10分
…………………10分
∴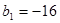
∴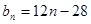 …………………12分
…………………12分
∴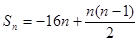 ×12=
×12= ……………14分
……………14分
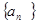 的公比为
的公比为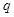 , ∴
, ∴ 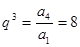
∴
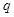 =2, ∴
=2, ∴ 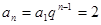
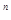
第二问由(1)得
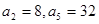 , ∴
, ∴ 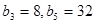
设
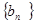 的公差为d, ∴
的公差为d, ∴ 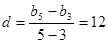
∴
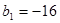 ∴
∴ 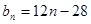 得到和式。
得到和式。解:设数列
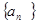 的公比为
的公比为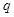 , ∴
, ∴ 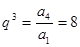 ·……………………3分
·……………………3分∴
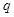 =2, ∴
=2, ∴ 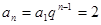
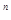 ……………………7分
……………………7分(2)由(1)得
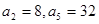 , ∴
, ∴ 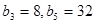
设
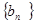 的公差为d, ∴
的公差为d, ∴ 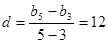 …………………10分
…………………10分∴
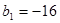
∴
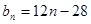 …………………12分
…………………12分∴
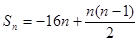 ×12=
×12= ……………14分
……………14分
练习册系列答案
相关题目
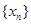 满足:
满足: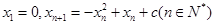
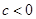
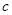 的取值范围,使数列
的取值范围,使数列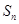 是等差数列
是等差数列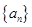 的前
的前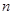 项和,且
项和,且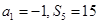 .
.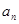 ;
;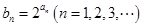 ,计算
,计算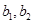 和
和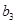 ,由此推测数列
,由此推测数列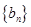 是等差数列还是等比数列,证明你的结论.
是等差数列还是等比数列,证明你的结论.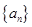 中,
中, ,
,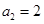 ,
,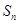 是数列
是数列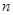 项和,且
项和,且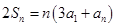 ,
,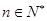 .
. 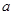 的值;
的值;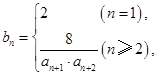
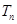 是数列
是数列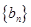 的前
的前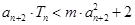 对一切
对一切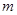 取值范围.
取值范围.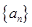 满足
满足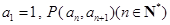 在直线
在直线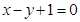 上,如果函数
上,如果函数
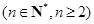 ,则函数
,则函数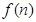 的最小值为
的最小值为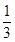
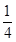
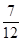
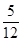
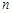 年(今年为第一年)的利润为
年(今年为第一年)的利润为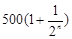 万元(
万元(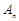 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为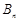 万元(需扣除技术改造资金).
万元(需扣除技术改造资金).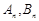 的表达式;
的表达式;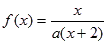 ,方程
,方程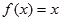 有唯一解,已知
有唯一解,已知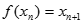
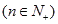 ,且
,且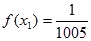 .
.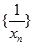 为等差数列,并求数列
为等差数列,并求数列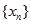 的通项公式;
的通项公式;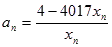 ,且
,且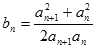
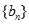 的前
的前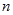 项和
项和 .
.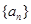 为等差数列,若
为等差数列,若 ,则
,则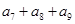 = ( )
= ( )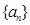 是等差数列, 若
是等差数列, 若 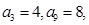 则
则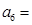 ( )
( )