题目内容
【题目】已知椭圆E： 
=1（a＞b＞0）的离心率e= 
，并且经过定点P（ 
， 
）． （Ⅰ）求椭圆E的方程；
（Ⅱ）问是否存在直线y=﹣x+m，使直线与椭圆交于A、B两点，满足OA⊥OB，若存在求m值，若不存在说明理由．
【答案】解：（Ⅰ）由题意：e= 
= 
，且 
， 解得：a=2，b=1，∴椭圆E的方程为 
（Ⅱ）设A（x1 ， y1），B（x2 ， y2）
由题意得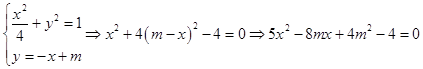 
（*）
所以 
= 
由 
得 
又方程（*）要有两个不等实根， 
m的值符合上面条件，所以 
【解析】（Ⅰ）利用椭圆E： 
=1（a＞b＞0）的离心率e= 
，并且经过定点P（ 
， 
），建立方程，求出a，b，即可求椭圆E的方程；（Ⅱ）直线y=﹣x+m代入椭圆方程，利用韦达定理，结合 
，即可求m值．
练习册系列答案
相关题目
