题目内容
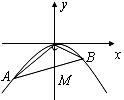
抛物线
上有两点A (x1, y1)，B (x2, y2)，且
= 0，又知点M (0, 2).
（1）求证：A、M、B三点共线； （2）若
，求AB所在的直线方程.
解：设
，∵
，∴
= 0 (x1x2≠0).
∴x1x2 = 4.
又∵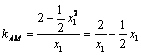
，
.
代
代入kAM得
，
∴A、M、B三点共线.
（2）∵
，∴
∴
，∴
. 即
或
.
∴
或
，AB的方程为
.
练习册系列答案
相关题目
题目内容
抛物线上有两点A (x1, y1)，B (x2, y2)，且= 0，又知点M (0, 2).
（1）求证：A、M、B三点共线； （2）若，求AB所在的直线方程.
解：设，∵，∴= 0 (x1x2≠0).
∴x1x2 = 4.
又∵，.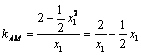
代代入kAM得，
∴A、M、B三点共线.
（2）∵，∴
∴，∴. 即或.
∴或，AB的方程为.
上有两点A、B,且|AB|=6.则线段AB的中点M到y轴的最小距离为 .
上有两点A、B，且AB垂直于y轴，若
，则抛物线的焦点到直线AB的距离是 （ ）
B、
C、
D、
上有两点A（x1，y1）、B（x2，y2），且
，又
．
；
，求AB所在直线方程．
上有两点A（x1，y1）、B（x2，y2），且
，又
．
；
，求AB所在直线方程．
上有两点A、B，且AB垂直于y轴，若
，则抛物线的焦点到直线AB的距离是（ ）
