题目内容
已知抛物线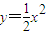 上有两点A、B,且AB垂直于y轴,若
上有两点A、B,且AB垂直于y轴,若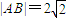 ,则抛物线的焦点到直线AB的距离是( )
,则抛物线的焦点到直线AB的距离是( )A.

B.

C.

D.

【答案】分析:先根据 ,根据抛物线的对称性,设A点的坐标为(
,根据抛物线的对称性,设A点的坐标为( ,n).代入抛物线方程得n的值,从而得出直线AB的方程,最后求出抛物线的焦点到直线AB的距离即可.
,n).代入抛物线方程得n的值,从而得出直线AB的方程,最后求出抛物线的焦点到直线AB的距离即可.
解答: 解:抛物线
解:抛物线 焦点为F(0,
焦点为F(0, ),
),
由于 ,根据抛物线的对称性,
,根据抛物线的对称性,
可设A点的坐标为( ,n).
,n).
代入抛物线方程得: ,∴n=1,
,∴n=1,
∴直线AB的方程为y=1,
则抛物线的焦点到直线AB的距离是1- =
= .
.
故选A.
点评:本题考查抛物线的标准方程,以及简单性质的应用,体现了数形结合的数学思想.
 ,根据抛物线的对称性,设A点的坐标为(
,根据抛物线的对称性,设A点的坐标为( ,n).代入抛物线方程得n的值,从而得出直线AB的方程,最后求出抛物线的焦点到直线AB的距离即可.
,n).代入抛物线方程得n的值,从而得出直线AB的方程,最后求出抛物线的焦点到直线AB的距离即可.解答:
 解:抛物线
解:抛物线 焦点为F(0,
焦点为F(0, ),
),由于
 ,根据抛物线的对称性,
,根据抛物线的对称性,可设A点的坐标为(
 ,n).
,n).代入抛物线方程得:
 ,∴n=1,
,∴n=1,∴直线AB的方程为y=1,
则抛物线的焦点到直线AB的距离是1-
 =
= .
.故选A.
点评:本题考查抛物线的标准方程,以及简单性质的应用,体现了数形结合的数学思想.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 上有一点
上有一点 到焦点
到焦点 的距离为5,
的距离为5, 及
及 的值。
的值。 交抛物线于A,B两点,若
交抛物线于A,B两点,若 ,求直线
,求直线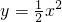 上有两点A、B,且AB垂直于y轴,若
上有两点A、B,且AB垂直于y轴,若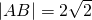 ,则抛物线的焦点到直线AB的距离是
,则抛物线的焦点到直线AB的距离是


