Question

（2012•自贡一模）已知

a

+

b

+

c

=

0

，且

a

与

c

的夹角为60°，|

b

|=

3

|

a

|，则cos＜

a

，

b

＞等于（　　）

• A．

  3

  2

• B．

  1

  2

• C．-

  1

  2

• D．-

  3

  2

Answer 1

分析：由题意可得-

b

=

a

+

c

，平方化简可得 |

c

| =| 

a

|，故以

a

、

c

 为邻边的平行四边形是一个菱形，从而得到

a

、

b

 的夹角等于150°，从而求得cos＜

a

，

b

＞的值．

解答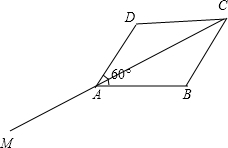：解：由题意可得-

b

=

a

+

c

，平方可得 3

a

2=

a

2+2

a

•

c

+

c

2=

a

2 +2|

a

|•|

c

|• cos60°+

c

2．
即2|

a

|2=|

a

|•|

c

|+|

c

|2，|

a

|2-|

c

|2=|

a

|•|

c

|-|

a

|2，
∴（|

a

|+|

c

|）（|

a

|-|

c

|）=|

a

|（|

c

|- |

a

|），
化简可得 （|

a

|-|

c

|）•（2|

a

|+|

c

|）=0，∴|

c

| =| 

a

|．
故以

a

、

c

 为邻边的平行四边形是一个菱形．
如图所示：设

AB

=

a

，

AD

=

c

，则

AC

=

a

+

c

，s设 

AM

=-

AC

，
由

a

 与

c

的夹角等于60°，可得∠BAD=60°，∠BAC=30°，故∠MAB=150°，即

a

、

b

 的夹角等于150°，
∴cos＜

a

，

b

＞=cos150°=-

3

2

，
故选D．

点评：本题主要考查两个向量的数量积的定义，判断以

a

、

c

 为邻边的平行四边形是一个菱形，是解题的关键，体现了数形结合的数学思想，属于中档题．