题目内容
(1)已知圆S:x2+y2=a2(a>0),直线l1:y=k1x+p交圆S于C、D两点,交直线l2:y=k2x于E点,若k1•k2=-1,证明:E是CD的中点;
(2)已知椭圆T:
+
=1(a>b>0),直线l1:y=k1x+p交椭圆T于C、D两点,交直线l2:y=k2x于E点,若k1•k2=-
.问E是否是CD的中点,若是,请给出证明;若不是,请说明理由.
(2)已知椭圆T:
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
分析:(1)联立直线l1,l2的方程,联立直线l1与圆的方程,确定CD中点坐标,利用韦达定理,即可得到结论;
(2)联立直线l1,l2的方程,联立直线l1与圆的方程,确定CD中点坐标,利用韦达定理,即可得到结论.
(2)联立直线l1,l2的方程,联立直线l1与圆的方程,确定CD中点坐标,利用韦达定理,即可得到结论.
解答:证明:(1)若k1•k2=-1,则l2:y=-
x,与l1:y=k1x+p联立解得xE=-
.
将l1:y=k1x+p与S:x2+y2=a2(a>0)联立消去y,整理得(1+k12)x2+2k1px+p2-a2=0,
设C(x1,y1),D(x2,y2),CD的中点为M(x0,y0),
则x0=
=
(-
)=-
=xE,
所以E与M重合,故E是CD的中点. …(8分)
(2)证明:若k1•k2=-
,则L2:y=-
x,与l1:y=k1x+p联立,解得xE=-
.
将l1:y=k1x+p与T:
+
=1(a>b>0)联立消去y,整理得(b2+a2k12)x2+2a2k1px+a2p2-a2b2=0
设C(x1,y1),D(x2,y2),CD的中点为M(x0,y0),
则x0=
=
(-
)=-
=xE,
所以E与M重合,故E是CD的中点. …(16分)
| 1 |
| k1 |
| k1p |
| 1+k12 |
将l1:y=k1x+p与S:x2+y2=a2(a>0)联立消去y,整理得(1+k12)x2+2k1px+p2-a2=0,
设C(x1,y1),D(x2,y2),CD的中点为M(x0,y0),
则x0=
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 2k1p |
| 1+k12 |
| k1p |
| 1+k12 |
所以E与M重合,故E是CD的中点. …(8分)
(2)证明:若k1•k2=-
| b2 |
| a2 |
| b2 |
| a2k1 |
| a2k1p |
| b2+a2k12 |
将l1:y=k1x+p与T:
| x2 |
| a2 |
| y2 |
| b2 |
设C(x1,y1),D(x2,y2),CD的中点为M(x0,y0),
则x0=
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 2a2k1p |
| b2+a2k12 |
| a2k1p |
| b2+a2k12 |
所以E与M重合,故E是CD的中点. …(16分)
点评:本题考查直线与直线,直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知圆
已知圆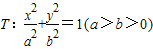 ,直线l1:y=k1x+p交椭圆T于C、D两点,交直线l2:y=k2x于E点,若
,直线l1:y=k1x+p交椭圆T于C、D两点,交直线l2:y=k2x于E点,若 .问E是否是CD的中点,若是,请给出证明;若不是,请说明理由.
.问E是否是CD的中点,若是,请给出证明;若不是,请说明理由.