题目内容
设抛物线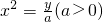 与直线y=kx+b交于两点,它们的横坐标分别是x1,x2,直线与x轴交点的横坐标是x3,那么x1,x2,x3的关系是
与直线y=kx+b交于两点,它们的横坐标分别是x1,x2,直线与x轴交点的横坐标是x3,那么x1,x2,x3的关系是
- A.x3=x1+x2
- B.x1x2=x2x3+x1x3
- C.
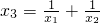
- D.x1x3=x2x3+x1x2
B
分析:抛物线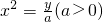 与直线y=kx+b交于两点,它们的横坐标分别是x1,x2,x1,x2是一元二次方程ax2-kx-b=0的两根,由韦达定理得:
与直线y=kx+b交于两点,它们的横坐标分别是x1,x2,x1,x2是一元二次方程ax2-kx-b=0的两根,由韦达定理得: ,又直线与x轴交点横坐标x3,所以x3=-
,又直线与x轴交点横坐标x3,所以x3=- ,于是x1x3+x2x3=(x1+x2)•x3=
,于是x1x3+x2x3=(x1+x2)•x3= ,即可得答案.
,即可得答案.
解答:∵抛物线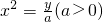 与直线y=kx+b交于两点,它们的横坐标分别是x1,x2,
与直线y=kx+b交于两点,它们的横坐标分别是x1,x2,
∴x1,x2是一元二次方程ax2-kx-b=0的两根,由韦达定理得: ,又直线与x轴交点横坐标x3,所以x3=-
,又直线与x轴交点横坐标x3,所以x3=- ,于是x1x3+x2x3=(x1+x2)•x3
,于是x1x3+x2x3=(x1+x2)•x3
= ,即x1x2=x2x3+x1x3.
,即x1x2=x2x3+x1x3.
故选B.
点评:本题考查直线与抛物线的位置关系,解题时要认真审题,仔细解答,注意合理地进行等价转化.
分析:抛物线
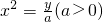 与直线y=kx+b交于两点,它们的横坐标分别是x1,x2,x1,x2是一元二次方程ax2-kx-b=0的两根,由韦达定理得:
与直线y=kx+b交于两点,它们的横坐标分别是x1,x2,x1,x2是一元二次方程ax2-kx-b=0的两根,由韦达定理得: ,又直线与x轴交点横坐标x3,所以x3=-
,又直线与x轴交点横坐标x3,所以x3=- ,于是x1x3+x2x3=(x1+x2)•x3=
,于是x1x3+x2x3=(x1+x2)•x3= ,即可得答案.
,即可得答案.解答:∵抛物线
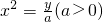 与直线y=kx+b交于两点,它们的横坐标分别是x1,x2,
与直线y=kx+b交于两点,它们的横坐标分别是x1,x2,∴x1,x2是一元二次方程ax2-kx-b=0的两根,由韦达定理得:
 ,又直线与x轴交点横坐标x3,所以x3=-
,又直线与x轴交点横坐标x3,所以x3=- ,于是x1x3+x2x3=(x1+x2)•x3
,于是x1x3+x2x3=(x1+x2)•x3=
 ,即x1x2=x2x3+x1x3.
,即x1x2=x2x3+x1x3.故选B.
点评:本题考查直线与抛物线的位置关系,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )为抛物线y2=kx-1与直线y=x的一个交点.
)为抛物线y2=kx-1与直线y=x的一个交点.