题目内容
已知α是三角形的一个内角，且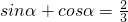
，则这个三角形是
- A.钝角三角形
- B.锐角三角形
- C.不等腰的直角三角形
- D.等腰直角三角形
A
分析：把所给的等式两边平方，得2sinαcosα=-
＜0，在三角形中，只能cosα＜0，只有钝角cosα＜0，故α为钝角，三角形形状得判．
解答：∵（sinα+cosα）2=
，∴2sinαcosα=-，
∵α是三角形的一个内角，∴sinα＞0，cosα＜0，
∴α为钝角，∴这个三角形为钝角三角形．
故选A．
点评：把和的形式转化为乘积的形式，易于判断三角函数的符号，进而判断出角的范围，最后得出三角形的形状．
分析：把所给的等式两边平方，得2sinαcosα=-
＜0，在三角形中，只能cosα＜0，只有钝角cosα＜0，故α为钝角，三角形形状得判．解答：∵（sinα+cosα）2=
，∴2sinαcosα=-，∵α是三角形的一个内角，∴sinα＞0，cosα＜0，
∴α为钝角，∴这个三角形为钝角三角形．
故选A．
点评：把和的形式转化为乘积的形式，易于判断三角函数的符号，进而判断出角的范围，最后得出三角形的形状．
练习册系列答案
相关题目
是三角形的一个内角，且
，则
的值为（ ）
B．
C．
D．