题目内容
分解因式:(1)2x2-7x+3;
(2)(x2+2x)2-7(x2+2x)-8;
(3)x2+2x-15-ax-5a.
【答案】分析:(1)由十字相乘法或求根公式法皆可分解因式.
(2)把x2+2x看做一个整体t,相当于先分解t2-7t-8,进而再进一步分解即可.
(3)先分组分解,把x2+2x-15与-ax-5a分成两组,再提取公因式即可.
解答:解:(1)由十字相乘法得:
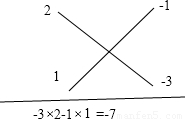
∴2x2-7x+3=(2x-1)(x-3).
(2)把x2+2x看做一个整体,则(x2+2x)2-7(x2+2x)-8=(x2+2x-8)(x2+2x+1)=(x+4)(x-2)(x+1)2.
(3)∵x2+2x-15=(x+5)(x-3),
∴x2+2x-15-ax-5a=(x+5)(x-3)-a(x+5)=(x+5)(x-3-a).
点评:利用十字相乘法和求根公式法是因式分解常用的方法,要求熟练掌握.
(2)把x2+2x看做一个整体t,相当于先分解t2-7t-8,进而再进一步分解即可.
(3)先分组分解,把x2+2x-15与-ax-5a分成两组,再提取公因式即可.
解答:解:(1)由十字相乘法得:

∴2x2-7x+3=(2x-1)(x-3).
(2)把x2+2x看做一个整体,则(x2+2x)2-7(x2+2x)-8=(x2+2x-8)(x2+2x+1)=(x+4)(x-2)(x+1)2.
(3)∵x2+2x-15=(x+5)(x-3),
∴x2+2x-15-ax-5a=(x+5)(x-3)-a(x+5)=(x+5)(x-3-a).
点评:利用十字相乘法和求根公式法是因式分解常用的方法,要求熟练掌握.

练习册系列答案
相关题目
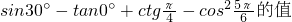 ,
,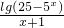 的定义域.
的定义域.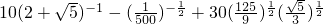 的值.
的值.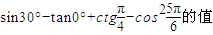 ,
,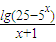 的定义域.
的定义域. 的值.
的值.