题目内容
已知向量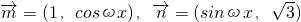 (ω>0),函数
(ω>0),函数 ,且f(x)图象上一个最高点为P
,且f(x)图象上一个最高点为P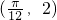 ,与P最近的一个最低点的坐标为
,与P最近的一个最低点的坐标为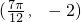 .
.
(1)求函数f(x)的解析式;
(2)设a为常数,判断方程f(x)=a在区间 上的解的个数;
上的解的个数;
(3)在锐角△ABC中,若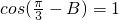 ,求f(A)的取值范围.
,求f(A)的取值范围.
解:(1)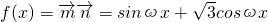 =
= =
=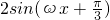 .…(3分)
.…(3分)
∵f(x)图象上一个最高点为P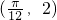 ,与P最近的一个最低点的坐标为
,与P最近的一个最低点的坐标为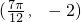 ,
,
∴ ,∴T=π,于是
,∴T=π,于是 .…(5分)
.…(5分)
所以 .…(6分)
.…(6分)
(2)当x∈ 时,
时,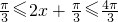 ,由
,由 图象可知:
图象可知:
当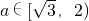 时,f(x)=a在区间
时,f(x)=a在区间 上有二解; …(8分)
上有二解; …(8分)
当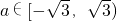 或a=2时,f(x)=a在区间
或a=2时,f(x)=a在区间 上有一解;
上有一解;
当 或a>2时,f(x)=a在区间
或a>2时,f(x)=a在区间 上无解.…(10分)
上无解.…(10分)
(3)在锐角△ABC中,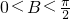 ,
,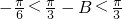 .
.
又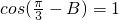 ,故
,故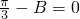 ,
, .…(11分)
.…(11分)
在锐角△ABC中, ,∴
,∴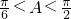 .…(13分)
.…(13分)
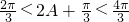 ,
,
∴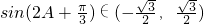 ,…(15分)
,…(15分)
∴
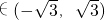 .
.
即f(A)的取值范围是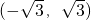 .…(16分)
.…(16分)
分析:(1)由已知中向量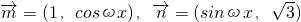 (ω>0),函数
(ω>0),函数 ,根据向量的数量积的定义,可得函数f(x)的解析式(含参数),进而根据f(x)图象上一个最高点为P
,根据向量的数量积的定义,可得函数f(x)的解析式(含参数),进而根据f(x)图象上一个最高点为P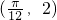 ,与P最近的一个最低点的坐标为
,与P最近的一个最低点的坐标为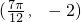 ,求出参数的值,即可得到答案.
,求出参数的值,即可得到答案.
(2)根据正弦型函数的图象和性质,分析函数f(x)在区间 上的图象和性质,即可得到答案.
上的图象和性质,即可得到答案.
(3)由锐角△ABC中,若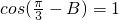 ,可以求出A的范围,结合(1)中函数的解析式可得f(A)的取值范围.
,可以求出A的范围,结合(1)中函数的解析式可得f(A)的取值范围.
点评:本题考查的知识点是平面向量的数量积运算,三角函数中的恒等变换,正弦型函数的图象和性质,其中根据已知条件,确定函数的解析式是解答本题的关键.
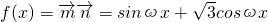 =
= =
=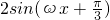 .…(3分)
.…(3分)∵f(x)图象上一个最高点为P
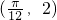 ,与P最近的一个最低点的坐标为
,与P最近的一个最低点的坐标为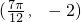 ,
,∴
 ,∴T=π,于是
,∴T=π,于是 .…(5分)
.…(5分)所以
 .…(6分)
.…(6分)(2)当x∈
 时,
时,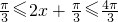 ,由
,由 图象可知:
图象可知:当
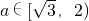 时,f(x)=a在区间
时,f(x)=a在区间 上有二解; …(8分)
上有二解; …(8分)当
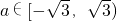 或a=2时,f(x)=a在区间
或a=2时,f(x)=a在区间 上有一解;
上有一解;当
 或a>2时,f(x)=a在区间
或a>2时,f(x)=a在区间 上无解.…(10分)
上无解.…(10分)(3)在锐角△ABC中,
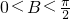 ,
,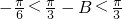 .
.又
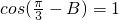 ,故
,故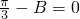 ,
, .…(11分)
.…(11分)在锐角△ABC中,
 ,∴
,∴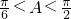 .…(13分)
.…(13分)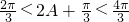 ,
,∴
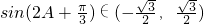 ,…(15分)
,…(15分)∴

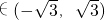 .
.即f(A)的取值范围是
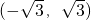 .…(16分)
.…(16分)分析:(1)由已知中向量
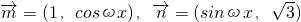 (ω>0),函数
(ω>0),函数 ,根据向量的数量积的定义,可得函数f(x)的解析式(含参数),进而根据f(x)图象上一个最高点为P
,根据向量的数量积的定义,可得函数f(x)的解析式(含参数),进而根据f(x)图象上一个最高点为P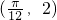 ,与P最近的一个最低点的坐标为
,与P最近的一个最低点的坐标为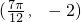 ,求出参数的值,即可得到答案.
,求出参数的值,即可得到答案.(2)根据正弦型函数的图象和性质,分析函数f(x)在区间
 上的图象和性质,即可得到答案.
上的图象和性质,即可得到答案.(3)由锐角△ABC中,若
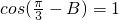 ,可以求出A的范围,结合(1)中函数的解析式可得f(A)的取值范围.
,可以求出A的范围,结合(1)中函数的解析式可得f(A)的取值范围.点评:本题考查的知识点是平面向量的数量积运算,三角函数中的恒等变换,正弦型函数的图象和性质,其中根据已知条件,确定函数的解析式是解答本题的关键.

练习册系列答案
相关题目