题目内容
下列四个命题，其中正确的是（ ）
①已知向量
和
，则“
•
=0”的充要条件是“
=
或
=
”；
②已知数列{an}和{bn}，则“
anbn=0”的充要条件是“
an=0或
bn=0”；
③已知z1，z2∈C，则“z1•z2=0”的充要条件是“z1=0或z2=0”；
④已知α，β∈R，则“sinα•cosβ=0”的充要条件是“α=kπ，（k∈Z）或β=
+kπ，(k∈Z)”
①已知向量
| α |
| β |
| α |
| β |
| α |
| 0 |
| β |
| 0 |
②已知数列{an}和{bn}，则“
| lim |
| n→∞ |
| lim |
| n→∞ |
| lim |
| n→∞ |
③已知z1，z2∈C，则“z1•z2=0”的充要条件是“z1=0或z2=0”；
④已知α，β∈R，则“sinα•cosβ=0”的充要条件是“α=kπ，（k∈Z）或β=
| π |
| 2 |
分析：根据向量垂直的充要条件，可以判断①；举出反例an=
，bn=
，可以判断②；根据复数乘法运算法则，及复数相等的充要条件，可判断③；根据三角函数的定义，可以判断④
|
|
解答：解：①已知向量
和
，则“
•
=0”的充要条件是“
=
或
=
或
⊥
”，故①错误；
②若数列an=
，bn=
，则“
anbn=0”但“
an=0与
bn=0”均不成立，故②错误；
③已知z1，z2∈C，则“z1•z2=0”的充要条件是“z1=0或z2=0”，故③正确；
④已知α，β∈R，则“sinα•cosβ=0”的充要条件是“sinα=0或cosβ=0”，即“α=kπ，（k∈Z）或β=
+kπ，(k∈Z)”，故④正确；
故正确的命题有③④
故选D
| α |
| β |
| α |
| β |
| α |
| 0 |
| β |
| 0 |
| α |
| β |
②若数列an=
|
|
| lim |
| n→∞ |
| lim |
| n→∞ |
| lim |
| n→∞ |
③已知z1，z2∈C，则“z1•z2=0”的充要条件是“z1=0或z2=0”，故③正确；
④已知α，β∈R，则“sinα•cosβ=0”的充要条件是“sinα=0或cosβ=0”，即“α=kπ，（k∈Z）或β=
| π |
| 2 |
故正确的命题有③④
故选D
点评：本题以命题的真假判断为载体，考查了向量垂直，数列极限，复数相等，三角函数的定义及充要条件等知识点，难度中档．
练习册系列答案
相关题目
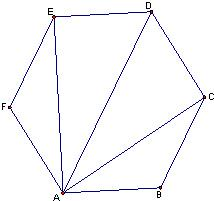如图，正六边形ABCDEF中，有下列四个命题：其中真命题的代号是
升水时，水面恰好经过正四棱锥的顶点P.如果将容器倒置，水面也恰好过点
（图2）.有下列四个命题：
，
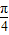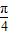]上是增函数；
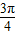对称．