题目内容
已知渐近线方程为y=±
的双曲线经过点(4,
),则双曲线的方程是( )
| x |
| 2 |
| 3 |
A、
| ||
B、x2+
| ||
C、y2-
| ||
D、
|
分析:由渐近线方程为y=±
可设所求的双曲线方程为
-
=λ (λ≠0),由双曲线经过点(4,
)
代入可得λ,从而可得所求的双曲线方程
| x |
| 2 |
| y2 |
| 1 |
| x2 |
| 4 |
| 3 |
代入可得λ,从而可得所求的双曲线方程
解答:解:渐近线方程为y=±
故可设所求的双曲线方程为
-
=λ (λ≠0)
双曲线经过点(4,
)
代入可得λ=-1
故所求的双曲线方程为
-y2=1
故选D.
| x |
| 2 |
故可设所求的双曲线方程为
| y2 |
| 1 |
| x2 |
| 4 |
双曲线经过点(4,
| 3 |
代入可得λ=-1
故所求的双曲线方程为
| x2 |
| 4 |
故选D.
点评:本题主要考查了双曲线的方程的求解解题的关键是需要由题意设出双曲线的方程,在双曲线的方程求解中,若已知双曲线方程
-
=1,可得渐近线方程为
-
=0;但若渐近线方程为程程为
-
=0可设双曲线方程为
-
=λ(λ≠0).
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 的双曲线经过点(4,
的双曲线经过点(4, ),则双曲线的方程是
),则双曲线的方程是 -x2=1
-x2=1 =1
=1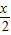 的双曲线经过点(4,
的双曲线经过点(4,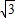 ),则双曲线的方程是( )
),则双曲线的方程是( )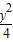 -x2=1
-x2=1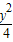 =1
=1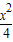 =1
=1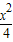 -y2=1
-y2=1