题目内容
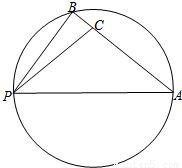
如图,点B在以PA为直径的圆周上,点C在线段AB上,已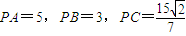 ,设∠APB=α,∠APC=β,α,β均为锐角.
,设∠APB=α,∠APC=β,α,β均为锐角.(1)求β;
(2)求向量
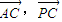 的数量积
的数量积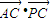 的值.
的值.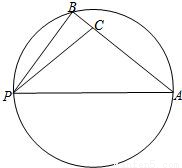
【答案】分析:(1)据圆周角为直角,通过解直角三角形及两角和的余弦公式及正余弦的平方公式求出α,α-β的正切,求出β的正切得角β.
(2)将未知向量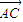 用已知向量
用已知向量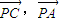 表示,利用向量的分配律求出数量积.
表示,利用向量的分配律求出数量积.
解答:解:(1):因为点B在以PA为直径的圆周上,所以∠ABP=90°,
所以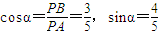 .
.
所以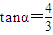 ,
,
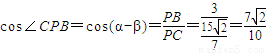 ,
, ,
,
所以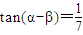 ,
,
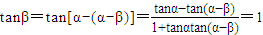 ,
,
又 ,所以
,所以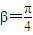 .
.
(2)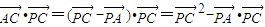
=
故答案为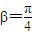 ;
;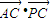 =
=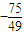
点评:本题考查解直角三角形;通过三角函数值求角;平面向量的基本定理;向量数量积的运算律等.
(2)将未知向量
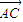 用已知向量
用已知向量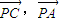 表示,利用向量的分配律求出数量积.
表示,利用向量的分配律求出数量积.解答:解:(1):因为点B在以PA为直径的圆周上,所以∠ABP=90°,
所以
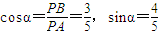 .
.所以
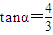 ,
,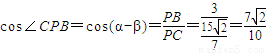 ,
, ,
,所以
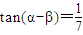 ,
,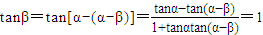 ,
,又
 ,所以
,所以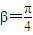 .
.(2)
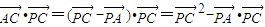
=

故答案为
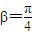 ;
;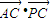 =
=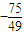
点评:本题考查解直角三角形;通过三角函数值求角;平面向量的基本定理;向量数量积的运算律等.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
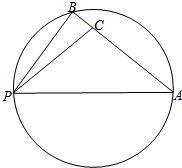 如图,点B在以PA为直径的圆周上,点C在线段AB上,已
如图,点B在以PA为直径的圆周上,点C在线段AB上,已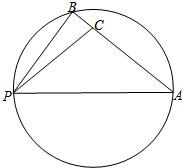
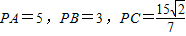 ,设∠APB=α,∠APC=β,α,β均为锐角.
,设∠APB=α,∠APC=β,α,β均为锐角.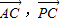 的数量积
的数量积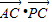 的值.
的值.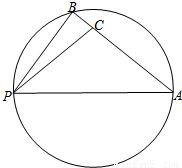
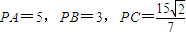 ,设∠APB=α,∠APC=β,α,β均为锐角.
,设∠APB=α,∠APC=β,α,β均为锐角.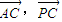 的数量积
的数量积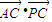 的值.
的值.