题目内容
18.椭圆$\frac{{x}^{2}}{3}$+y2=1的一个焦点坐标为( )| A. | ($\sqrt{2}$,0) | B. | (0,$\sqrt{2}$) | C. | (2,0) | D. | (0,2) |
分析 求出椭圆的a,b,由c=$\sqrt{{a}^{2}-{b}^{2}}$,求得c,即可得到焦点坐标.
解答 解:椭圆$\frac{{x}^{2}}{3}$+y2=1的a=$\sqrt{3}$,b=1,
c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{2}$,
则椭圆的焦点为($-\sqrt{2}$,0),($\sqrt{2}$,0),
故选:A.
点评 本题考查椭圆的方程和性质,主要考查椭圆的焦点坐标,属于基础题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
8.对椭圆C1;$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和椭圆C2;$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1(a>b>0)的几何性质的表述正确的是( )
| A. | 范围相同 | B. | 顶点坐标相同 | C. | 焦点坐标相同 | D. | 离心率相同 |
13.将单位正方体放置在水平桌面上(一面与桌面完全接触),沿其一条棱翻动一次后,使得正方体的另一面与桌面完全接触,称一次翻转.如图,正方体的顶点 A,经任意翻转三次后,点 A与其终结位置的直线距离不可能为( )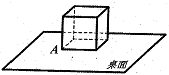

| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
10.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F1,作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
7.双曲线C:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1的左、右顶点分别为A1,A2,点P在C上且直线PA2的斜率的取值范围是($\frac{1}{2}$,1),那么直线PA1斜率的取值范围是( )
| A. | ($\frac{1}{3}$,$\frac{3}{4}$) | B. | ($\frac{3}{4}$,$\frac{5}{2}$) | C. | ($\frac{1}{3}$,$\frac{5}{2}$) | D. | ($\frac{5}{4}$,$\frac{5}{2}$) |