题目内容
已知圆C的半径为2,圆心在x轴的正半轴上,直线 与圆C相切.
与圆C相切.
(I)求圆C的方程;
(II)过点Q(0,-3)的直线 与圆C交于不同的两点A
与圆C交于不同的两点A 、B
、B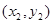 ,当
,当 时,求△AOB的面积.
时,求△AOB的面积.
【答案】
(1)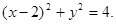
(2)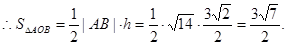
【解析】
试题分析:解:(I)设圆心为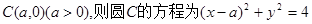 ,
,
因为圆C与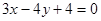 相切,
相切,
所以 ,
,
解得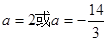 (舍去),
(舍去),
所以圆C的方程为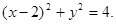 4分
4分
(II)显然直线l的斜率存在,设直线l的方程为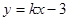 ,
,
由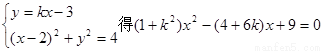 ,
,
∵直线l与圆相交于不同两点
 ,
,
设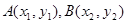 ,则
,则
 , ①
, ①
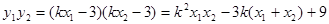 ,
,
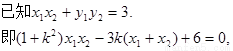
将①代入并整理得 ,
,
解得k = 1或k =-5(舍去),
所以直线l的方程为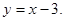 8分
8分
圆心C到l的距离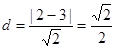 ,
,
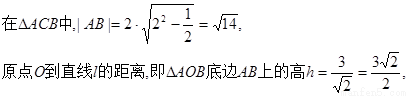
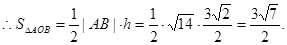
考点:直线与圆的位置关系
点评:主要是考查了直线与圆的位置关系的运用,属于中档题。

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知圆C的半径为2,圆心在x轴的正半轴上,直线3x+4y+4=0与圆C相切,则圆C的方程为( )
| A、x2+y2-2x-3=0 | B、x2+y2+4x=0 | C、x2+y2+2x-3=0 | D、x2+y2-4x=0 |
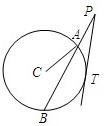 (选做题)(几何证明选讲)如图所示,过圆C外一点P做一条直线与圆C交于A,B两点,BA=2AP,PT与圆C相切于T点.已知圆C的半径为2,∠CAB=30°,则PT=
(选做题)(几何证明选讲)如图所示,过圆C外一点P做一条直线与圆C交于A,B两点,BA=2AP,PT与圆C相切于T点.已知圆C的半径为2,∠CAB=30°,则PT=