题目内容
已知圆C的半径为2,圆心C在x轴的正半轴上,直线3x-4y+4=0与圆C相切.
(Ⅰ)求圆C的方程;
(Ⅱ)是否存在过点P(0,-3)的直线l与圆C交于不同两点A、B,且弦AB的垂直平分线m过点Q(3,-3),若存在,求出直线l的方程;若不存在,请说明理由.
(Ⅰ)求圆C的方程;
(Ⅱ)是否存在过点P(0,-3)的直线l与圆C交于不同两点A、B,且弦AB的垂直平分线m过点Q(3,-3),若存在,求出直线l的方程;若不存在,请说明理由.
分析:(Ⅰ)利用直线与圆相切的性质即可求出;
(Ⅱ)利用点到直线的距离公式、直线与圆相交得到直线l满足的条件,再利用线段的垂直平分线的性质及垂径定理及推论即可得出.
(Ⅱ)利用点到直线的距离公式、直线与圆相交得到直线l满足的条件,再利用线段的垂直平分线的性质及垂径定理及推论即可得出.
解答:解:(I)设圆心为C(a,0)(a>0),则圆C的方程为(x-a)2+y2=4
∵圆C与3x-4y+4=0相切,∴
=2,即|3a+4|=10,
解得a=2或a=-
(舍去),
∴圆C的方程为(x-2)2+y2=4.
(II)假设符合条件的直线l存在,显然直线l的斜率存在,设直线l的方程为y=kx-3,
∵直线l与圆相交于不同两点,则圆心C到直线l的距离d=
<r=2,解得k>
,
直线m的方程为y+3=-
(x-3),即x+ky+3k-3=0.
由于直线m垂直平分弦AB,故圆心C(2,0)必在直线m上,解得k=
.
而
∉(
,+∞),
故不存在直线l,使得过点Q(3,-3)的直线m垂直平分弦AB.
∵圆C与3x-4y+4=0相切,∴
| |3a+4| | ||
|
解得a=2或a=-
| 14 |
| 3 |
∴圆C的方程为(x-2)2+y2=4.
(II)假设符合条件的直线l存在,显然直线l的斜率存在,设直线l的方程为y=kx-3,
∵直线l与圆相交于不同两点,则圆心C到直线l的距离d=
| |2k-3| | ||
|
| 5 |
| 12 |
直线m的方程为y+3=-
| 1 |
| k |
由于直线m垂直平分弦AB,故圆心C(2,0)必在直线m上,解得k=
| 1 |
| 3 |
而
| 1 |
| 3 |
| 5 |
| 12 |
故不存在直线l,使得过点Q(3,-3)的直线m垂直平分弦AB.
点评:熟练掌握直线与圆相切的性质、点到直线的距离公式、直线与圆相交满足的条件、线段的垂直平分线的性质及垂径定理及推论是解题的关键.

练习册系列答案
相关题目
已知圆C的半径为2,圆心在x轴的正半轴上,直线3x+4y+4=0与圆C相切,则圆C的方程为( )
| A、x2+y2-2x-3=0 | B、x2+y2+4x=0 | C、x2+y2+2x-3=0 | D、x2+y2-4x=0 |
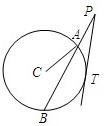 (选做题)(几何证明选讲)如图所示,过圆C外一点P做一条直线与圆C交于A,B两点,BA=2AP,PT与圆C相切于T点.已知圆C的半径为2,∠CAB=30°,则PT=
(选做题)(几何证明选讲)如图所示,过圆C外一点P做一条直线与圆C交于A,B两点,BA=2AP,PT与圆C相切于T点.已知圆C的半径为2,∠CAB=30°,则PT= 与圆C相切.
与圆C相切. 与圆C交于不同的两点A
与圆C交于不同的两点A 、B
、B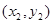 ,当
,当 时,求△AOB的面积.
时,求△AOB的面积.