题目内容
下列说法中:
①函数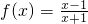 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点;
②若定义在R上的函数f(x)满足f(x+2)=-f(x-1),则函数f(x)周期为6;
③若对于任意x∈(1,3),不等式x2-ax+2<0恒成立,则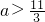 ;
;
④函数y=log2(x2-ax-a)的值域为R,则a∈(-4,0);
其中正确命题的序号为 ________(把所有正确命题的序号都填上)
①②
分析:①考查方程f(x)=g(x)解的个数
②推导f(x+6)=f(x)
③转化为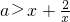 在(1,3)上恒成立,从而转化为求
在(1,3)上恒成立,从而转化为求
④x2-ax-a可取所有正数,△=a2+4a≥0
解答:①令f(x)=g(x)? ,可得方程无解即图象无交点,①正确
,可得方程无解即图象无交点,①正确
②由f(x+2)=-f(x-1)可得f(x+3)=-f(x)?f(x+6)=f(x),从而可得函数的周期为6,②正确
③由任意x∈(1,3),不等式x2-ax+2<0恒成立?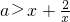 在(1,3)上恒成立,故
在(1,3)上恒成立,故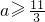 ③错误
③错误
④函数y=log2(x2-ax-a)的值域为R,可得△=a2+4a≥0则a∈[0,+∞)∪(-∞,-4]④错误
故答案为①②
点评:本题综合考查了函数的性质:周期、最值问题、对数函数的值域问题.解题中用到的数学思想有:方程与函数的思想,等价转化的思想.
分析:①考查方程f(x)=g(x)解的个数
②推导f(x+6)=f(x)
③转化为
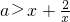 在(1,3)上恒成立,从而转化为求
在(1,3)上恒成立,从而转化为求
④x2-ax-a可取所有正数,△=a2+4a≥0
解答:①令f(x)=g(x)?
 ,可得方程无解即图象无交点,①正确
,可得方程无解即图象无交点,①正确②由f(x+2)=-f(x-1)可得f(x+3)=-f(x)?f(x+6)=f(x),从而可得函数的周期为6,②正确
③由任意x∈(1,3),不等式x2-ax+2<0恒成立?
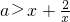 在(1,3)上恒成立,故
在(1,3)上恒成立,故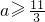 ③错误
③错误④函数y=log2(x2-ax-a)的值域为R,可得△=a2+4a≥0则a∈[0,+∞)∪(-∞,-4]④错误
故答案为①②
点评:本题综合考查了函数的性质:周期、最值问题、对数函数的值域问题.解题中用到的数学思想有:方程与函数的思想,等价转化的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点;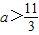 ;
; 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点; ;
;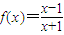 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点;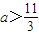 ;
;