题目内容
已知函数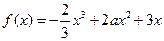 .
.
(Ⅰ)当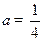 时,求函数
时,求函数 在
在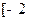 ,
, 上的最大值、最小值;
上的最大值、最小值;
(Ⅱ)令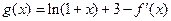 ,若
,若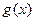 在
在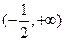 上单调递增,求实数
上单调递增,求实数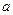 的取值范围.
的取值范围.

考察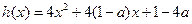 的对称轴为
的对称轴为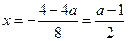
(i) 当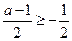 ,即
,即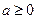 时,应有
时,应有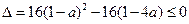
解得: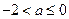 ,所以
,所以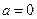 时成立…………9分
时成立…………9分
(ii) 当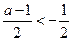 ,即
,即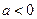 时,应有
时,应有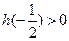 即:
即: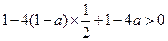
解得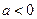 …………11分
…………11分
综上:实数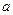 的取值范围是
的取值范围是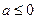 …………12分
…………12分
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知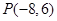 是角终边上一点,则
是角终边上一点,则 的值等于( )
的值等于( )
A. | B. | C. | D. |
若 是定义在R上的连续函数,且
是定义在R上的连续函数,且 ,则
,则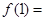 ( )
( )
| A.2 | B.1 | C.0 | D.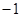 |
 分13分)已知
分13分)已知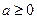 ,函数
,函数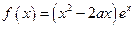 .
.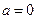 时讨论函数的单调性;
时讨论函数的单调性;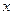 取何值时,
取何值时,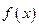 取最小值,证明你的结论.
取最小值,证明你的结论. 某厂家拟在2012年举行促销活动,经调查测算,该产品的
某厂家拟在2012年举行促销活动,经调查测算,该产品的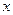 万件与年促销费用
万件与年促销费用 万元(
万元( (
( 为
为 两部分资金).
两部分资金). 润最大?
润最大? ,则
,则 .
.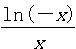 ,其中e是自然常数,a∈R.
,其中e是自然常数,a∈R. x)的单调性、极值;
x)的单调性、极值; 的图象过点(1, -4),且函数
的图象过点(1, -4),且函数 的图象关于y轴对称.
的图象关于y轴对称. 的极值;
的极值; 在区间
在区间 上的最大值。
上的最大值。 在点
在点 处连续,则常
处连续,则常 的值是 ( )
的值是 ( ) 2
2  3
3  4
4  5
5