题目内容
下面三个判断中,正确的是①f(n)=1+k+k2+…+kn(n∈N*),当n=1时,f(n)=1;
②f(n)=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
③f(n)=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n+1 |
| 1 |
| 3k+2 |
| 1 |
| 3k+3 |
| 1 |
| 3k+4 |
分析:本题考查的知识点为简单的合情推理,根据式中定义对各个式子进行分类讨论,即可得到答案.
解答:解:①中n=1时,f(n)=f(1)=1+k不等于1,
故①不正确;
②中n=1时,f(1)=1+
+
,故②正确;
③中f(k+1)=f(k)+
+
+
-
,
故③不正确
故答案为:②
故①不正确;
②中n=1时,f(1)=1+
| 1 |
| 2 |
| 1 |
| 3 |
③中f(k+1)=f(k)+
| 1 |
| 3k+2 |
| 1 |
| 3k+3 |
| 1 |
| 3k+4 |
| 1 |
| k+1 |
故③不正确
故答案为:②
点评:这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 +
+ +…+
+…+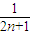 (n∈N*),当n=1时,f(n)=1+
(n∈N*),当n=1时,f(n)=1+ +
+ ;
;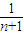 +
+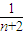 +…+
+…+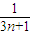 (n∈N*),则f(k+1)=f(k)+
(n∈N*),则f(k+1)=f(k)+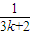 +
+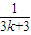 +
+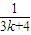 .
. +
+ +…+
+…+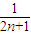 (n∈N*),当n=1时,f(n)=1+
(n∈N*),当n=1时,f(n)=1+ +
+ ;
;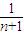 +
+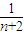 +…+
+…+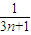 (n∈N*),则f(k+1)=f(k)+
(n∈N*),则f(k+1)=f(k)+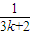 +
+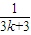 +
+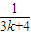 .
.